搜索
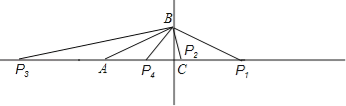
【题目】如图，已知在RtABC中，∠C=90°，∠A=30°，在直线AC上找点P，使△ABP是等腰三角形，则∠APB的度数为_______________
参考答案：
【答案】15°，30°，75°，120°
【解析】试题分析：∵在Rt△ABC中，∠C=90°，∠A=30°，
∴当AB=BP1时，∠BAP1=∠BP1A=30°，
当AB=AP3时，∠ABP3=∠AP3B=
∠BAC=×30°=15°，
当AB=AP2时，∠ABP2=∠AP2B=
×（180°﹣30°）=75°，
当AP4=BP4时，∠BAP4=∠ABP4，
∴∠AP4B=180°﹣30°×2=120°，
∴∠APB的度数为：15°、30°、75°、120°．
考点: 等腰三角形的判定
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c经过△ABC的三个顶点，与y轴相交于（0，
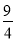），点A坐标为（﹣1，2），点B是点A关于y轴的对称点，点C在x轴的正半轴上．（1）求该抛物线的函数关系表达式．
（2）点F为线段AC上一动点，过F作FE⊥x轴，FG⊥y轴，垂足分别为E、G，当四边形OEFG为正方形时，求出F点的坐标．
（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动，设平移的距离为t，正方形的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求t的值；若不存在请说明理由．
-
科目： 来源： 题型：
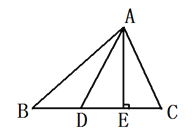
查看答案和解析>>【题目】（7分）如图，已知AE⊥BC，AD平分∠BAE，∠ADB=110°，∠CAE=20°．求∠B的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=2x2 - 4x+c经过点(2, -3),则c的值为( )
A.-1B.2C.-3D.-2
-
科目： 来源： 题型：
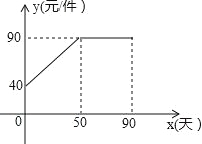
查看答案和解析>>【题目】九年级（3）班数学兴趣小组经过市场调查整理出某种商品在第x天（1≤x≤90，且x为整数）的售价与销售量的相关信息如下．已知商品的进价为30元/件，设该商品的售价为y（单位：元/件），每天的销售量为p（单位：件），每天的销售利润为w（单位：元）．
时间x（天）
1
30
60
90
每天销售量p（件）
198
140
80
20
（1）求出w与x的函数关系式；
（2）问销售该商品第几天时，当天的销售利润最大？并求出最大利润；
（3）该商品在销售过程中，共有多少天每天的销售利润不低于5600元？请直接写出结果．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图的方格中，每个小正方形的边长都为1，△ABC的顶点均在格点上．在建立平面直角坐标系后，点B的坐标为（﹣1，2）．
（1）把△ABC向下平移8个单位后得到对应的△A1B1C1，画出△A1B1C1；
（2）画出与△A1B1C1关于y轴对称的△A2B2C2；
（3）若点P（a，b）是△ABC边上任意一点，P2是△A2B2C2边上与P对应的点，写出P2的坐标为 ；
（4）试在y轴上找一点Q(在图中标出来)，使得点Q到B2、C2两点的距离之和最小，并求出QB2+QC2的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线y=（x﹣1）2+2的对称轴是（ ）
A.直线x=2
B.直线x=﹣2
C.直线x=1
D.直线x=﹣1
相关试题
