【题目】如图,△ABC是边长为5cm的等边三角形,点P,Q分别从顶点A,B同时出发,沿线段AB,BC运动,且它们的速度都为1cm/s.当点P到达点B时,P,Q两点停止运动,设点P的运动时间为t(s).

(1)当t为何值时,△PBQ是直角三角形?
(2)连接AQ、CP,相交于点M,则点P,Q在运动的过程中,∠CMQ会变化吗?若变化,则说明理由;若不变,请求出它的度数.
参考答案:
【答案】(1)当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形;(2)∠CMQ=60°不变,理由详见解析.
秒时,△PBQ为直角三角形;(2)∠CMQ=60°不变,理由详见解析.
【解析】
(1)需要分类讨论:分∠PQB=90°和∠BPQ=90°两种情况;
(2)∠CMQ=60°不变.通过证△ABQ≌△CAP(SAS)得到:∠BAQ=∠ACP,由三角形外角定理得到∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
(1)设时间为t,则AP=BQ=t,PB=5-t,
①当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,得5-t=2t,t=![]() ;
;
②当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(5-t),t=![]() ;
;
∴当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形;
秒时,△PBQ为直角三角形;
(2)∠CMQ=60°不变.
在△ABQ与△CAP中,
 ,
,
∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP,
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,若一弹簧长度(cm)与所挂物体质量(kg)之间的关系如下表:
物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
则下列说法错误的是( )
A.弹簧长度随物体的质量的变化而变化,物体的质量是自变量,弹簧的长度是因变量
B.如果物体的质量为x kg,那么弹簧的长度y cm可以表示为y=12+0.5x
C.在弹簧能承受的范围内,当物体的质量为7kg时,弹簧的长度为16cm
D.在没挂物体时,弹簧的长度为12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区域为响应“绿水青山就是金山银山”的号召,加强了绿化建设.为了解该区域群众对绿化建设的满意程度,某中学数学兴趣小组在该区域的甲、乙两个片区进行了调查,得到如下不完整统计图.
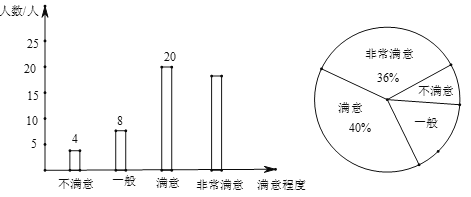
请结合图中信息,解决下列问题:
(1)此次调查中接受调查的人数为 人,其中“非常满意”的人数为 人;
(2)兴趣小组准备从“不满意”的4位群众中随机选择2位进行回访,已知这4位群众中有2位来自甲片区,另2位来自乙片区,请用画树状图或列表的方法求出选择的群众来自甲片区的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的外接圆
的外接圆 的直径,点P在BC延长线上,且满足
的直径,点P在BC延长线上,且满足 .
.(1)求证:PA是
 的切线;
的切线;(2)弦
 交
交 于点F,若
于点F,若 ,求AC的长.
,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中,装有红球、白球、黄球共12个,这些球除颜色外完全相同,
从中随机摸出一个球,则:
(1)若盒子中有红球3个,则摸到红球的概率为_________;
(2)若摸到黄球的概率为
 ,则该盒子中装有黄球的个数是__________个;
,则该盒子中装有黄球的个数是__________个;(3)若将这12个球分别标上1至12这十二个数字,则摸到的数字是0的概率为________;摸到的数字是偶数的概率为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,点
,点 是
是 边上的一个动点(点
边上的一个动点(点 不与点
不与点 ,点
,点 重合),在
重合),在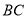 上取一点
上取一点 ,且∠CDE=50°.
,且∠CDE=50°.
(1)当
 时,求证:
时,求证: ;
;(2)当
 是等腰三角形时,
是等腰三角形时, 的度数为
的度数为
相关试题

