【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.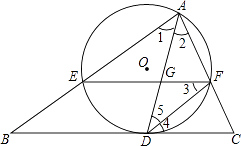
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长.
参考答案:
【答案】
(1)证明:连接OD, 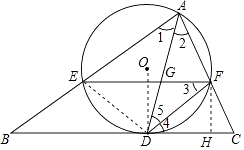
∵AD是△ABC的角平分线,
∴∠1=∠2,
∴ ![]() =
= ![]() ,
,
∴OD⊥EF,
∵EF∥BC,
∴OD⊥BC,
∴BC是⊙O的切线
(2)解:连接DE,
∵ ![]() =
= ![]() ,
,
∴DE=DF,
∵EF∥BC,
∴∠3=∠4,
∵∠1=∠3,
∴∠1=∠4,
∵∠DFC=∠AED,
∴△AED∽△DFC,
∴ ![]() ,即
,即 ![]() ,
,
∴DE2=36,
∴DE=6
(3)解:过F作FH⊥BC于H,
∵∠BAC=60°,
∴∠1=∠2=∠3=∠4=30°,
∴FH= ![]() DF=
DF= ![]() =3,DH=3
=3,DH=3 ![]() ,
,
∴CH= ![]() =
= ![]() ,
,
∵EF∥BC,
∴∠C=∠AFE,
∴tan∠AFE=tan∠C= ![]() =
= ![]() ;
;
∵∠4=∠2.∠C=∠C,
∴△ADC∽△DFC,
∴ ![]() ,
,
∵∠5=∠5,∠3=∠2,
∴△ADF∽△FDG,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DG= ![]() .
.
【解析】(1)连半径,证垂直。连接OD,由AD是△ABC的角平分线。得出圆周角相等,继而得弧相等,根据垂径定理得出OD⊥EF,再根据EF∥BC,得到OD⊥BC,即可得证。
(2)先证明DE=DF,再证明△AED∽△DFC,根据相似三角形的性质得对应边成比例,即可求出DE的长。
(3)抓住已知∠BAC=60°,既可以证得∠4=30°,由此添加辅助线过F作FH⊥BC于H,Rt△DFH和Rt△FHC中就可以求出线段FH、DH、CH的长,根据平行得角相等,即可求出an∠AFE的值,再证明△ADC∽△DFC和△ADF∽△FDG,找到中间比,继而就可以求出DG的长。
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的判定定理的理解,了解切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以
 等为代表的战略性新兴产业.据统计,目前广东
等为代表的战略性新兴产业.据统计,目前广东 基站的数量约
基站的数量约 万座,计划到2020年底,全省
万座,计划到2020年底,全省 基站数量是目前的
基站数量是目前的 倍,到2022年底,全省
倍,到2022年底,全省 基站数量将达到
基站数量将达到 万座.
万座. 计划到2020年底,全省
计划到2020年底,全省 基站的数量是多少万座?
基站的数量是多少万座? 按照计划,求2020年底到2022年底,全省
按照计划,求2020年底到2022年底,全省 基站数量的年平均增长率;
基站数量的年平均增长率; 求2021年底全省
求2021年底全省 基站的数量.
基站的数量. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫的惠农富农,老张在科技人员的指导下,改良柑橘品种,去年他家的柑橘喜获丰收,而且质优味美,客商闻讯前来采购,经协商:采购价y(元/吨)与采购量x(吨)之间的函数关系如图所示.

(1)求y与x之间的函数关系式;
(2)老张种植柑橘的成本是800元/吨,当客商采购量是多少时,老张在这次销售柑橘时获利最大?最大利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?
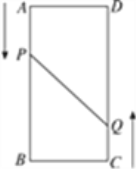
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照有关规定,距高铁轨道
 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形
米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形 为一新建小区,直线
为一新建小区,直线 为高铁轨道,
为高铁轨道, 是直线
是直线 上的两点,点
上的两点,点 在一条直线上,且
在一条直线上,且 .小王看中了
.小王看中了 号楼
号楼 单元的一套住宅,与售楼人员的对话如下:
单元的一套住宅,与售楼人员的对话如下: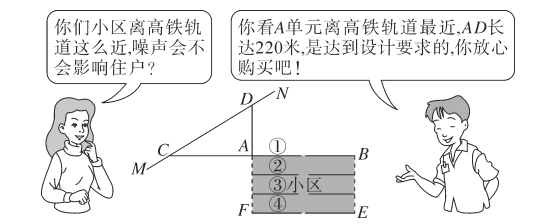
 小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由; 若一列长度为
若一列长度为 米的高铁以
米的高铁以 千米/时的速度通过,则
千米/时的速度通过,则 单元用户受到影响的时间有多长?
单元用户受到影响的时间有多长?(参考数据:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )

A.128°
B.126°
C.122°
D.120°
相关试题

