【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD,BE,CE,若∠CBD=32°,则∠BEC的度数为( )
A.128°
B.126°
C.122°
D.120°
参考答案:
【答案】C
【解析】解:在⊙O中,∵∠CBD=32°,
∵∠CAD=32°,
∵点E是△ABC的内心,
∴∠BAC=64°,
∴∠EBC+∠ECB=(180°﹣64°)÷2=58°,
∴∠BEC=180°﹣58°=122°.
所以答案是:C.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对圆周角定理的理解,了解顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,以AD为弦的⊙O交AB,AC于E,F,已知EF∥BC.
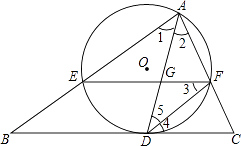
(1)求证:BC是⊙O的切线;
(2)若已知AE=9,CF=4,求DE长;
(3)在(2)的条件下,若∠BAC=60°,求tan∠AFE的值及GD长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c交x轴于A(﹣4,0),B(1,0),交y轴于C点,且OC=2OB.

(1)求抛物线的解析式;
(2)在直线BC上找点D,使△ABD为以AB为腰的等腰三角形,求D点的坐标.
(3)在抛物线上是否存在异于B的点P,过P点作PQ⊥AC于Q,使△APQ与△ABC相似?若存在,请求出P点坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】按照有关规定,距高铁轨道
 米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形
米以内的区域内不宜临路新建学校、医院、敬老院和集中住宅区等噪声敏感建筑物.如图是一个小区平面示意图,长方形 为一新建小区,直线
为一新建小区,直线 为高铁轨道,
为高铁轨道, 是直线
是直线 上的两点,点
上的两点,点 在一条直线上,且
在一条直线上,且 .小王看中了
.小王看中了 号楼
号楼 单元的一套住宅,与售楼人员的对话如下:
单元的一套住宅,与售楼人员的对话如下: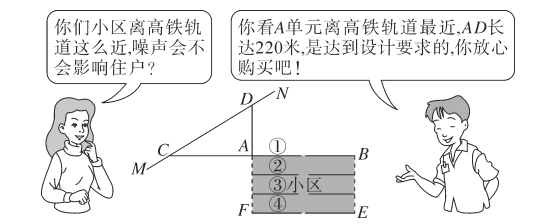
 小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由;
小王心中一算,发现售楼人员的话不可信,请你用所学的数学知识说明理由; 若一列长度为
若一列长度为 米的高铁以
米的高铁以 千米/时的速度通过,则
千米/时的速度通过,则 单元用户受到影响的时间有多长?
单元用户受到影响的时间有多长?(参考数据:
 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ?

-
科目: 来源: 题型:
查看答案和解析>>【题目】温度的变化是人们经常谈论的话题,请根据图象与同伴讨论某天温度变化的情况.
(1)这一天的最高温度是多少?是在几时到达的?最低温度呢?
(2)这一天的温差是多少?从最低温度到最高温度经过多长时间?
(3)在什么时间范围内温度在上升?在什么时间范围内温度在下降?
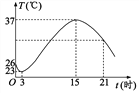
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:某校一块长为2a米的正方形空地是七年级四个班的清洁区,其中分给七年级(1)班的清洁区是一块边长为(a-2b)米的正方形,(0<b<
 ).
).(1)分别求出七(2)、七(3)班的清洁区的面积;
(2)七(4)班的清洁区的面积比七(1)班的清洁区的面积多多少平方米.

相关试题

