【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

参考答案:
【答案】17, 48
【解析】
首先确定小华所搭几何体所需的正方体的个数,然后确定两人共搭建几何体所需小立方体的数量,求差即可;
分别得到前后面,上下面,左右面的面积,相加即可求解.
∵小华所搭几何体恰好可以和小颖所搭几何体拼成一个无缝隙的大正方体,
∴该正方体需要小立方体3×3×3=27个,
∵小颖用10个边长为1的小正方体搭成了一个几何体,
∴小华至少还需27-10=17个小立方体,
表面积为:2×(8+8+8)=48,
故答案为:17,48.
-
科目: 来源: 题型:
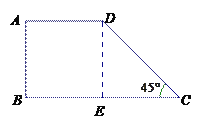
查看答案和解析>>【题目】为了增强学生体质,学校鼓励学生多参加体育锻炼,小华同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED为正方形,∠DCE=45°,AB=100米.小华某天绕该道路晨跑5圈,求小华该天晨跑的路程是多少?(结果保留整数,
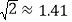 )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种型号的滑板车,共花费13000元,所购进甲型车的数量不少于乙型车数量的二倍,但不超过乙型车数量的三倍.现已知甲型车每辆进价200元,乙型车每辆进价400元,设商店购进乙型车x辆.
(1)商店有哪几种购车方案?
(2)若商店将购进的甲、乙两种型号的滑板车全部售出,并且销售甲型车每辆获得利润70元,销售乙型车每辆获得利润50元,写出此商店销售这两种滑板车所获得的总利润y(元)与购进乙型车的辆数x(辆)之间的函数关系式?并求出商店购进乙型车多少辆时所获得的利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
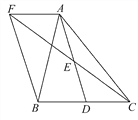
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)-3+8-11-15 (2)

(3)
 (4)
(4)
(5)0.125×(-7)×8 (6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE

(1)求证:AB是⊙O的切线;
(2)过D点作DF∥BC交⊙O于点F,求线段DF的长.
相关试题

