【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
参考答案:
【答案】(1)回到了球门线的位置(2 )12米(3)58米
【解析】试题分析:(1)将各数进行相加,看结果是否为零,如果结果为零就说明回到了球门线的位置;(2)根据有理数的加法计算法则求出每次离球门线的距离,然后进行比较大小;(3)将各数的绝对值进行相加,得出答案.
试题解析:⑴、(+5)+(-3)+(+10)+(-8)+(-6)+(+12)+(-10)=0,
∴守门员最后正好回到了球门线的位置.
⑵、5+(-3)=2 2+10=12 12+(-8)=4 4+(-6)=-2 -2+12=10 10+(-10)=0
∴守门员离开球门线距离最远是12米.
⑶、![]() =54
=54
答:他共跑了54米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:

(1)20筐白菜中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2.6元,则出售这20筐白菜可卖多少元?(结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC,CB(或它们的延长线)于E、F,当∠EDF绕D点旋转到DE⊥AC于E时(如图1),
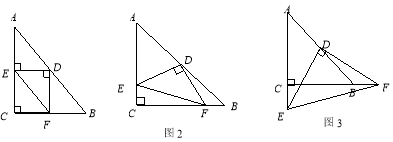
(1)易证
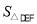 +
+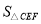 =
=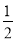
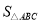 .
. (2)当∠EDF绕
(2)当∠EDF绕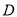 点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,
点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,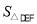 、
、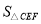 、
、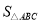 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】李明到离家2.1千米的学校参加初三联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即匀速步行回家,在家拿道具用了1分钟,然后立即匀速骑自行车返回学校.已知李明骑自行车到学校比他从学校步行到家用时少20分钟,且骑自行车的速度是步行速度的3倍.
(1)李明步行的速度(单位:米/分)是多少?
(2)李明能否在联欢会开始前赶到学校?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)当销售单价为70元时,每天的销售利润是多少?
(2)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并求出自变量
 的取值范围;
的取值范围;(3)如果该企业每天的总成本不超过7000元,那么销售单价为多少元时,每天的销售利润最大?最大利润是多少?(每天的总成本=每件的成本×每天的销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图抛物线
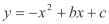 与
与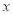 轴交于A(1,0),
轴交于A(1,0), 两点
两点 
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交
 轴于
轴于 点,在该抛物线的对称轴上是否存在点
点,在该抛物线的对称轴上是否存在点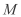 ,使得
,使得 的周长最小?若存在,求出
的周长最小?若存在,求出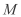 点的坐标;若不存在,请说明理由。
点的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】大润发超市进了一批成本为8元/个的文具盒。调查发现: 这种文具盒每个星期的销售量
 个)与它的定价
个)与它的定价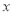 (元/个)的关系如图所示:
(元/个)的关系如图所示: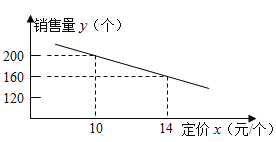
(1)求这种文具盒每个星期的销售量
 个)与它的定价
个)与它的定价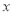 (元/个)之间的函数关系式(不必写出自变量
(元/个)之间的函数关系式(不必写出自变量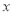 的取值范围)
的取值范围)(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
相关试题

