【题目】如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE
(1)求证:AB是⊙O的切线;
(2)过D点作DF∥BC交⊙O于点F,求线段DF的长.
参考答案:
【答案】
(1)
解:如图,连接OB、OE.
在△ABO和△EBO中,
∵ 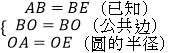 ,
,
∴△ABO≌△EBO(SSS),
∴∠BAO=∠BEO(全等三角形的对应角相等);
又∵BE是⊙O的切线,
∴OE⊥BC,
∴∠BEO=90°,
∴∠BAO=90°,即AB⊥AD,
∴AB是⊙O的切线;
(2)
解:
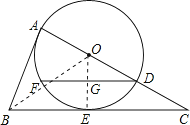
∵AD=10,DC=8,
∴OC=13,OE=5,
∴在直角△OEC中,根据勾股定理知,EC=12.
设DF交OE于点G.
∵DF∥BC(已知),
∴∠OGD=∠OEC=90°(两直线平行,同位角相等),
∴OG⊥DF,
∴FD=2DG(垂径定理);
∵DF∥BC,
∴ ![]() ,即
,即 ![]() ,
,
∴DG= ![]() ,
,
∴DF= ![]() .
.
【解析】(1)欲证AB是⊙O的切线,只需证明证得AB⊥AD即可;(2)根据垂径定理推知DF=2DG;然后根据平行线截线段成比例证得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,由此可以求得DF的长度.
,由此可以求得DF的长度.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

-
科目: 来源: 题型:
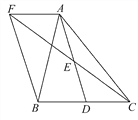
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)-3+8-11-15 (2)

(3)
 (4)
(4)
(5)0.125×(-7)×8 (6)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,
 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,
, 分别是线段
分别是线段 ,
, 的中点.
的中点.(1)求证:
 ≌
≌ ;
;(2)判断四边形
 是什么特殊四边形,并证明你的结论;
是什么特殊四边形,并证明你的结论;(3)当四边形
 是正方形时,求
是正方形时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(-
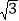 ,0),B(0,1)分别为x轴,y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0),B(0,1)分别为x轴,y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
A.
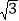 B.
B.  C.
C.  D. 2
D. 2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂生产某品牌的护眼灯,并将护眼灯按质量分成15个等级(等级越高,灯的质量越好.如:二级产品好于一级产品).若出售这批护眼灯,一级产品每台可获利润21元,每提高一个等级每台可多获利润1元,工厂每天只能生产同一个等级的护眼灯,每个等级每天生产的台数如下表所示:
等级(x级)
一级
二级
三级
…
生产量(y台/天)
78
76
74
…
(1)已知护眼灯每天的生产量y(台)是等级x(级)的一次函数,请直接写出y与x之间的函数关系式:;
(2)若工厂将当日所生产的护眼灯全部售出,工厂应生产哪一等级的护眼灯,才能获得最大利润?最大利润是多少?
相关试题

