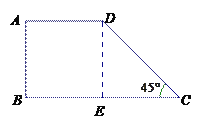
【题目】为了增强学生体质,学校鼓励学生多参加体育锻炼,小华同学马上行动,每天围绕小区进行晨跑锻炼.该小区外围道路近似为如图所示四边形ABCD,已知四边形ABED为正方形,∠DCE=45°,AB=100米.小华某天绕该道路晨跑5圈,求小华该天晨跑的路程是多少?(结果保留整数,![]() )
)
参考答案:
【答案】小华该天晨跑的路程约为2705米
【解析】分析:由正方形的性质得△DEC是等腰直角三角形,然后利用勾股定理求出CD的长度,然后求出小胖每天晨跑的路程.
详解:∵四边形ABCD是正方形,∴DE=AB=BE=AD=100,
∠DEC=∠DEB=90°,又∵∠DCE=45°,
∴△DEC是等腰直角三角形,
∴EC=DE=100,
∴DC=![]() ,
,
5(AB+BC+CD+AD)=5(100+100+100+![]() +100)
+100)
=5(400+![]() )
)
≈2705(米),
∴小华该天晨跑的路程约为2705米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】同学们都知道,
 表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:
表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离,试探索:(1)求
 =________.
=________.(2)若
 =5,则x=____.
=5,则x=____.(3)同理
 表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-1和2所对应的两点距离之和,请你找出所有符合条件的整数x,使得 =3,这样的整数是________(直接写答案)
=3,这样的整数是________(直接写答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先观察下列等式,再完成题后问题:
 ,
, ,
,
①请你猜想:
 =________.
=________.②若a、b为有理数,且
 ,
,求:
 +…+
+…+ 的值.
的值.(2)探究并计算:
 +
+ +
+ +…+
+…+
(3)如图,把一个面积为1的正方形等分成两个面积为
 的长方形,接着把面积为
的长方形,接着把面积为 的长方形等分成两个面积为
的长方形等分成两个面积为 的正方形,再把面积为
的正方形,再把面积为 的正方形等分成两个面积为
的正方形等分成两个面积为 的矩形.如此进行下去,试利用图形揭示的规律计算:
的矩形.如此进行下去,试利用图形揭示的规律计算: +
+ +
+ +
+ +
+ +
+ +
+ .(直接写答案).
.(直接写答案).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了更好地活跃校园文化生活,拟对本校自办的“辉煌”校报进行改版.先从全校学生中随机抽取一部分学生进行了一次问卷调查,题目为“你最喜爱校报的哪一个板块”(每人只限选一项).问卷收集整理后绘制了不完整的频数分布表和如图扇形统计图.
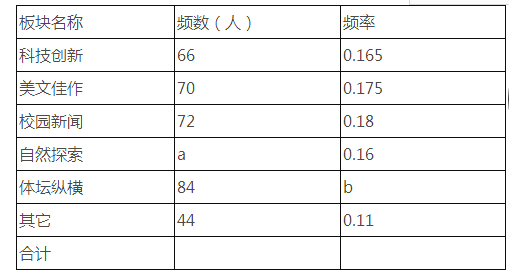
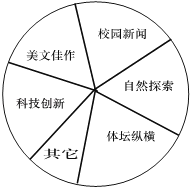
(1)填空:频数分布表中a= , b=;
(2)“自然探索”板块在扇形统计图中所占的圆心角的度数为;
(3)在参加此次问卷调查的学生中,最喜爱哪一个板块的人数最多?有多少人喜欢?
(4)若全校有1500人,估计喜欢“校园新闻”板块的有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进甲、乙两种型号的滑板车,共花费13000元,所购进甲型车的数量不少于乙型车数量的二倍,但不超过乙型车数量的三倍.现已知甲型车每辆进价200元,乙型车每辆进价400元,设商店购进乙型车x辆.
(1)商店有哪几种购车方案?
(2)若商店将购进的甲、乙两种型号的滑板车全部售出,并且销售甲型车每辆获得利润70元,销售乙型车每辆获得利润50元,写出此商店销售这两种滑板车所获得的总利润y(元)与购进乙型车的辆数x(辆)之间的函数关系式?并求出商店购进乙型车多少辆时所获得的利润最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

相关试题

