【题目】(1)-3+8-11-15 (2)![]()
(3)![]() (4)
(4)![]()
(5)0.125×(-7)×8 (6)![]()
参考答案:
【答案】(1)-21;(2)13;(3)2;(4)0;(5)-7;(6)9.
【解析】
(1)先将减法转化为加法,然后利用加法法则以及加法的运算律进行计算即可;
(2)写成代数和的形式,然后再运用法则进行即可;
(3)先化简绝对值,然后再进行有理数乘法运算即可;
(4)根据几个因数相乘,有一个因数为0,则结果为0直接即可得出结果;
(5)根据有理数乘法法则进行计算即可得答案;
(6)利用分配律进行计算即可得.
(1)原式= -3+8+(-11)+(-15)=5+(-26)= -21;
(2) 原式= ![]() =10+3=13;
=10+3=13;
(3) 原式=![]() =2;
=2;
(4)原式=0;
(5)原式= ![]() =-7;
=-7;
(6)原式=![]()
![]()
![]() = =12 + (-9) - (-6)=9 .
= =12 + (-9) - (-6)=9 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下:(单位:米)+5,-3,+10,-8,-6,+12,-10
(1)守门员最后是否回到了球门线的位置?
(2)在练习过程中,守门员离开球门最远距离是多少米?
(3)守门员全部练习结束后,他共跑了多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一次数学活动课上,小颖用 10 个棱长为 1 的正方体积木搭成一个几何体,然后她请小华用其 他棱长为 1 的正方体积木在旁边再搭一个几何体,使用小华所搭几何体恰好和小颖所搭几何体拼成一个 无空隙的大正方体(不改变小颖所搭几何体的形状).那么:按照小颖的要求搭几何体,小华至少需要_____个正方体积木.按照小颖的要求,小华所搭几何体的表面积最小为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
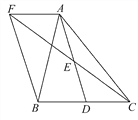
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是AC边上一点,AD=10,DC=8.以AD为直径的⊙O与边BC切于点E,且AB=BE

(1)求证:AB是⊙O的切线;
(2)过D点作DF∥BC交⊙O于点F,求线段DF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,
 ,
, 分别是边
分别是边 ,
, 的中点,
的中点, ,
, 分别是线段
分别是线段 ,
, 的中点.
的中点.(1)求证:
 ≌
≌ ;
;(2)判断四边形
 是什么特殊四边形,并证明你的结论;
是什么特殊四边形,并证明你的结论;(3)当四边形
 是正方形时,求
是正方形时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A(-
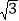 ,0),B(0,1)分别为x轴,y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0),B(0,1)分别为x轴,y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
A.
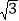 B.
B.  C.
C.  D. 2
D. 2
相关试题

