【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.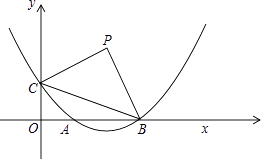
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.
参考答案:
【答案】
(1)
解:∵抛物线y=ax2﹣4ax+1,
∴点C的坐标为(0,1).
∵OB=3OC,
∴点B的坐标为(3,0).
∴9a﹣12a+1=0,
∴ ![]() .
.
∴ ![]() .
.
(2)
解:如图,
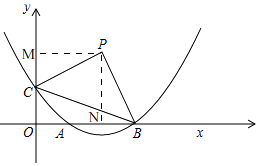
过点P作PM⊥y轴,PN⊥x轴,垂足分别为点M、N.
∵∠MPC=90°﹣∠CPN,∠NPB=90°﹣∠CPN,
∴∠MPC=∠NPB.
在△PCM和△PBN中, 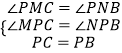 ,
,
∴△PMC≌△PNB,
∴PM=PN.
设点P(a,a).
∵PC2=PB2,
∴a2+(a﹣1)2=(a﹣3)2+a2.
解得a=2.
∴P(2,2)
(3)
解:∵该抛物线对称轴为x=2,B(3,0),
∴A(1,0).
∵P(2,2),A(1,0),B(3,0),C(0,1),
∴PO= ![]() ,AC=
,AC= ![]() ,AB=2.
,AB=2.
∵∠CAB=135°,∠POB=45°,
在Rt△BOC中,tan∠OBC= ![]() ,
,
∴∠OBC≠45°,∠OCB<90°,
在Rt△OAC中,OC=OA,
∴∠OCA=45°,
∴∠ACB<45°,
∴当△OPQ与△ABC相似时,点Q只有在点O左侧时.
(i)当 ![]() 时,∴
时,∴ ![]() ,
,
∴OQ=4,
∴Q(﹣4,0).
(ii)当 ![]() 时,∴
时,∴ ![]() ,
,
∴OQ=2,
∴Q(﹣2,0).
当点Q在点A右侧时,
综上所述,点Q的坐标为(﹣4,0)或(﹣2,0).

【解析】(1)利用待定系数法即可得出结论;(2)先判断出△PMC≌△PNB,再用PC2=PB2 , 建立方程求解即可;(3)先判断出点Q只能在点O左侧,再分两种情况讨论计算即可.
【考点精析】利用二次函数的概念和二次函数的图象对题目进行判断即可得到答案,需要熟知一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y=
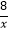 的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C. 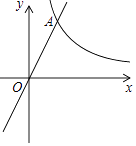
(1)求平移后直线的表达式;
(2)求∠OBC的余切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:
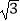 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 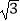 ≈1.73.)
≈1.73.)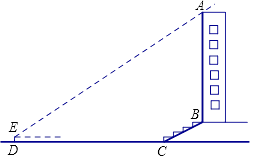
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
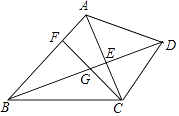
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB. -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法中,错误的是( )
A.抛物线于x轴的一个交点坐标为(﹣2,0)
B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )
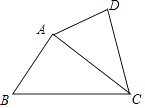
A.∠DAC=∠ABC
B.AC是∠BCD的平分线
C.AC2=BC?CD
D.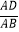 =
= 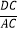
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE∥BC,且过△ABC的重心,分别与AB,AC交于点D,E,点P是线段DE上一点,CP的延长线交AB于点Q,如果
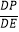 =
=  ,那么S△DPQ:S△CPE的值是 .
,那么S△DPQ:S△CPE的值是 . 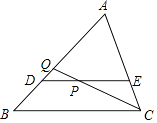
相关试题

