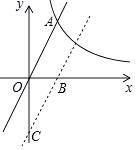
【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y= ![]() 的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C.
的图象与正比例函数y=kx(k≠0)的图象相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0),与y轴交于点C. 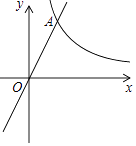
(1)求平移后直线的表达式;
(2)求∠OBC的余切值.
参考答案:
【答案】
(1)解:当x=2时,y= ![]() =4,
=4,
∴点A的坐标为(2,4).
∵A(2,4)在y=kx(k≠0)的图象上,
∴4=2k,解得:k=2.
设直线BC的函数解析式为y=2x+b,
∵点B的坐标为(3,0),
∴0=2×3+b,解得:b=﹣6,
∴平移后直线的表达式y=2x﹣6
(2)解:当x=0时,y=﹣6,
∴点C的坐标为(0,﹣6),
∴OC=6.
∴ ![]()
【解析】(1)根据点A在反比例函数图象上可求出点A的坐标,进而可求出正比例函数表达式,根据平移的性质可设直线BC的函数解析式为y=2x+b,根据点B的坐标利用待定系数法即可求出b值,此题得解;(2)利用一次函数图象上点的坐标特征即可求出点C的坐标,从而得出OC的值,再根据余切的定义即可得出结论.
【考点精析】本题主要考查了坐标与图形变化-平移和解直角三角形的相关知识点,需要掌握新图形的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点;连接各组对应点的线段平行且相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.
-
科目: 来源: 题型:
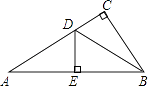
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是 .
-
科目: 来源: 题型:
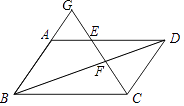
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E在边AD上,联结CE并延长,交对角线BD于点F,交BA的延长线于点G,如果DE=2AE,那么CF:EF:EG= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,将△ABC绕点A顺时针旋转,使点C落在边AB上的点E处,点B落在点D处,连接BD,如果∠DAC=∠DBA,那么
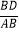 的值是 .
的值是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校兴趣小组想测量一座大楼AB的高度.如图6,大楼前有一段斜坡BC,已知BC的长为12米,它的坡度i=1:
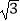 .在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,
.在离C点40米的D处,用测角仪测得大楼顶端A的仰角为37°,测角仪DE的高为1.5米,求大楼AB的高度约为多少米?(结果精确到0.1米) (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 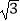 ≈1.73.)
≈1.73.)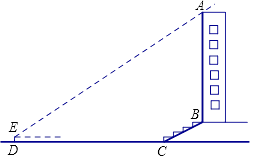
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD.
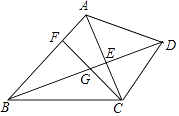
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+1与x轴的正半轴交于点A和点B,与y轴交于点C,且OB=3OC,点P是第一象限内的点,连接BC,△PBC是以BC为斜边的等腰直角三角形.
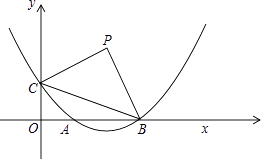
(1)求这个抛物线的表达式;
(2)求点P的坐标;
(3)点Q在x轴上,若以Q、O、P为顶点的三角形与以点C、A、B为顶点的三角形相似,求点Q的坐标.
相关试题

