【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .

参考答案:
【答案】![]() .
.
【解析】
试题过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,

∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=2,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]()
,即DQ+PQ的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=
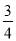 ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索:
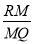 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,三个内角的平分线交于点
中,三个内角的平分线交于点 .过点
.过点 作
作 ,交边
,交边 于点
于点 .
.
(1)如图1,
①若
 ,则
,则 ___________,
___________, _____________;
_____________;②猜想
 与
与 的关系,并说明你的理由:
的关系,并说明你的理由:(2)如图2,作
 外角
外角 的平分线交
的平分线交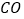 的延长线于点
的延长线于点 .若
.若 ,
, ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2x+5=3(x-1)
(2)
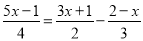
(3)
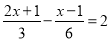
(4)
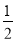 x+2
x+2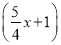 =8+x.
=8+x. -
科目: 来源: 题型:
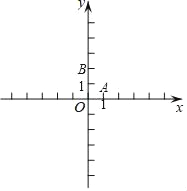
查看答案和解析>>【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=
 +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC
 DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )

A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是“作一个30°角”的尺规作图过程.
已知:平面内一点A.
求作:∠A,使得∠A
 30°.
30°.作法:如图,
(1)作射线AB;
(2)在射线AB上取一点O,以O为圆心,OA为半径作圆,与射线AB相交于点C;
 (3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.
(3)以C为圆心,OC为半径作弧,与⊙O交于点D,作射线AD.∠DAB即为所求的角.
请回答:该尺规作图的依据是 .
相关试题

