【题目】![]() 中,三个内角的平分线交于点
中,三个内角的平分线交于点![]() .过点
.过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .
.

(1)如图1,
①若![]() ,则
,则![]() ___________,
___________,![]() _____________;
_____________;
②猜想![]() 与
与![]() 的关系,并说明你的理由:
的关系,并说明你的理由:
(2)如图2,作![]() 外角
外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() .若
.若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)①![]() ,
,![]() ;②
;②![]() ,见解析;(2)
,见解析;(2)![]() .
.
【解析】
(1)①根据三角形的内角和得到∠BAC+∠BCA=180°-40°=140°,根据角平分线的定义得到∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,根据三角形的内角和即可得到结论;
(∠BAC+∠BCA)=70°,根据三角形的内角和即可得到结论;
②设∠ABC=α,根据三角形的内角和和角平分线的定义即可得到结论;
(2)根据角平分线的定义和三角形外角的性质即可得到结论.
(1)①∵∠ABC=40°,
∴∠BAC+∠BCA=180°-40°=140°,
∵△ABC中,三个内角的平分线交于点O,
∴∠OAC+∠OCA=![]() (∠BAC+∠BCA)=70°,
(∠BAC+∠BCA)=70°,
∴∠AOC=180°-70°=110°,
∵OB平分∠ABC,
∴∠ABO=![]() ∠ABC=20°,
∠ABC=20°,
∵OD⊥OB,
∴∠BOD=90°,
∴∠BDO=70°,
∴∠ADO=110°,
故答案为:110°,110°,
②相等,理由设∠ABC=α,
∴∠BAC+∠BCA=180°-α,
∵△ABC中,三个内角的平分线交于点O,
∴∠OAC+∠OCA=![]() (∠BAC+∠BCA)=90°-
(∠BAC+∠BCA)=90°-![]() α,
α,
∴∠AOC=180°-(∠OAC+∠OCA)=90°+![]() α,
α,
∵OB平分∠ABC,
∴∠ABO=![]() ∠ABC=
∠ABC=![]() α,
α,
∵OD⊥OB,
∴∠BOD=90°,
∴∠BDO=90°-![]() α,
α,
∴∠ADO=180°-∠BOD=90°+![]() α,
α,
∴∠AOC=∠ADO;
(2)由(1)知,∠ADO=∠AOC=105°,
∵BF平分∠ABE,CF平分∠ACB,
∴∠FBE=![]() ∠ABE,∠FCB=
∠ABE,∠FCB=![]() ∠ACB,
∠ACB,
∴∠FBE=∠F+∠FCB=![]() (∠BAC+∠ACB)=
(∠BAC+∠ACB)=![]() ∠BAC+∠FCB,
∠BAC+∠FCB,
∴∠BAC=2∠F=64°,
∴∠DAO=![]() ∠BAC=32°,
∠BAC=32°,
∴∠AOD=180°-∠ADO-∠DAO=43°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数
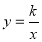 (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )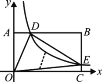
A.
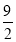 B.
B.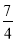 C.
C.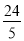 D.12
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥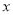 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=
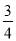 ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索:
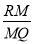 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2x+5=3(x-1)
(2)
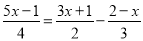
(3)
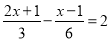
(4)
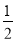 x+2
x+2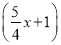 =8+x.
=8+x. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy(如图)中,已知抛物线y=
 +bx+c点经过A(1,0)、B(0,2).
+bx+c点经过A(1,0)、B(0,2).(1)求该抛物线的表达式;
(2)设该抛物线的对称轴与x轴的交点为C,第四象限内的点D在该抛物线的对称轴上,如果以点A、C、D所组成的三角形与△AOB相似,求点D的坐标;
(3)设点E在该抛物线的对称轴上,它的纵坐标是1,联结AE、BE,求sin∠ABE.
相关试题

