【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;0≤x≤
;0≤x≤![]() .
.
【解析】试题分析:(1)由正方形的性质及![]() 可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△
可求出BC=8,PC=6,由勾股定理可求出BP=10,再由△![]() ∽△
∽△![]() 即可求出结论;
即可求出结论;
(2)由正方形的性质得∠A=∠ABC=∠C=90°,由MQ∥AB得∠QMR=∠A,故∠QMR=∠C;由MQ∥AB得![]() ,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故
,而∠1+∠RQM=90°,∠ABP+∠PBC=90°,故![]() ,从而△
,从而△![]() ∽△
∽△![]() .故可得出结论;
.故可得出结论;
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,通过证明
,通过证明![]() ,分别计算
,分别计算![]() 及
及![]() ,
, ![]() ,从而可得出结论.
,从而可得出结论.
试题解析:(1)由题意,得![]() ,
,![]()
在Rt△![]() 中,
中, ![]()
∴![]()
∵![]()
∴![]() ∴
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴![]()
∴![]()
(2)答: ![]() 的比值随点
的比值随点![]() 的运动没有变化
的运动没有变化
理由:如图,
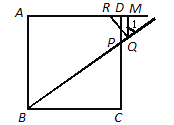
∵![]() ∥
∥![]()
∴![]() ,
, ![]()
∵![]()
∴![]()
∵![]()
∴![]()
![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
∴![]() 的比值随点
的比值随点![]() 的运动没有变化,比值为
的运动没有变化,比值为![]()
(3)延长![]() 交
交![]() 的延长线于点
的延长线于点![]()
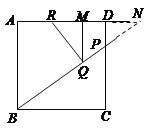
∵![]() ∥
∥![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ∥
∥![]() ,
, ![]() ∥
∥![]()
∴![]() ∥
∥![]()
∴![]()
∵![]() ,
, ![]()
∴![]()
又![]() ,
, ![]()
∴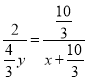
∴![]()
它的定义域是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】小莉的爸爸买了某演唱会的一张门票,她和哥哥两人都想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字 1,2,3,5 的四张牌给小莉,将数字为 4,6,7,8 的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后 将抽出的两张牌数字相加,如果和为偶数,则小莉去,如果和为奇数,则哥哥去。
(1)请用树状图或列表的方法表示出两张牌数字相加和的所有可能出现的结果;
(2)哥哥设计的游戏规则公平么?请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数
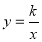 (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )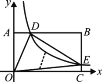
A.
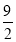 B.
B.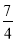 C.
C.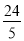 D.12
D.12 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个反比例函数
 和
和 在第一象限内的图象如图所示,点P在
在第一象限内的图象如图所示,点P在 的图象上,PC⊥
的图象上,PC⊥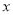 轴于点C,交
轴于点C,交 的图象于点A,PC⊥
的图象于点A,PC⊥ 轴于点D,交
轴于点D,交 的图象于点B. 当点P在
的图象于点B. 当点P在 的图象上运动时,以下结论:
的图象上运动时,以下结论:①

②
 的值不会发生变化
的值不会发生变化③PA与PB始终相等
④当点A是PC的中点时,点B一定是PD的中点.
其中一定不正确的是( )

A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 中,三个内角的平分线交于点
中,三个内角的平分线交于点 .过点
.过点 作
作 ,交边
,交边 于点
于点 .
.
(1)如图1,
①若
 ,则
,则 ___________,
___________, _____________;
_____________;②猜想
 与
与 的关系,并说明你的理由:
的关系,并说明你的理由:(2)如图2,作
 外角
外角 的平分线交
的平分线交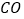 的延长线于点
的延长线于点 .若
.若 ,
, ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2x+5=3(x-1)
(2)
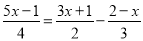
(3)
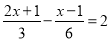
(4)
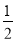 x+2
x+2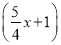 =8+x.
=8+x. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .

相关试题

