【题目】如图1,将![]() 纸片沿中位线
纸片沿中位线![]() 折叠,使点
折叠,使点![]() 的对称点
的对称点![]() 落在
落在![]() 边上,再将纸片分别沿等腰
边上,再将纸片分别沿等腰![]() 和等腰
和等腰![]() 的底边上的高线
的底边上的高线![]() ,
,![]() 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.
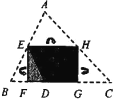
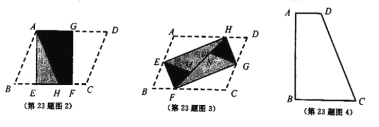
(1)将![]() 纸片按图2的方式折叠成一个叠合矩形
纸片按图2的方式折叠成一个叠合矩形![]() ,则操作形成的折痕分别是线段_____,_____;
,则操作形成的折痕分别是线段_____,_____;![]() ______.
______.
(2)![]() 纸片还可以按图3的方式折叠成一个叠合矩形
纸片还可以按图3的方式折叠成一个叠合矩形![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
(3)如图4,四边形![]() 纸片满足
纸片满足![]() .小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出
.小明把该纸片折叠,得到叠合正方形.请你帮助画出叠合正方形的示意图,并求出![]() 的长.
的长.
参考答案:
【答案】(1)(1)AE;GF;1:2;(2)13;(3)按图1的折法,则AD=1,BC=7;按图2的折法,则AD=![]() ,BC=
,BC=![]() .
.
【解析】
试题分析:(1)由图2观察可得出答案为AE,GF,由折叠的轴对称性质可得出答案为1:2;(2)由EF和EH的长度根据勾股定理可求出FH的长度,再由折叠的轴对称性质易证△AEH≌△CGF;再根据全等三角形的性质可得出AD的长度;(3)由折叠的图可分别求出AD和BC的长度.
试题解析:(1)AE;GF;1:2
(2)解:∵四边形EFGH是叠合矩形,∠FEH=90°,EF=5,EH=12;
∴FH=![]() =13;
=13;
由折叠的轴对称性可知:DH=NH,AH=HM,CF=FN;
易证△AEH≌△CGF;
∴CF=AH;
∴AD=DH+AH=HN+FN=FH=13.
(3)解:本题有以下两种基本折法,如图1,图2所示.
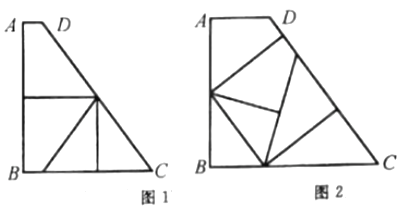
按图1的折法,则AD=1,BC=7.
按图2的折法,则AD=![]() ,BC=
,BC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级全体男同学参加了跳绳比赛,从中随机抽取某班男同学的跳绳成绩,制作了如下频数分布表:
组别
99.5﹣109.5
109.5﹣119.5
119.5﹣129.5
129.5﹣139.5
139.5﹣149.5
149.5﹣159.5
频数
2
4
8
7
3
1
根据上面统计信息,解答下列问题:
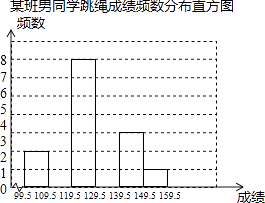
(1)补全频数分布直方图.
(2)班级准备对跳绳成绩优秀的男同学进行奖励,奖励人数占班级男同学的20%,该班张辉同学的成绩为140个,通过计算判断张辉能否获得奖励.
(3)八年级共有200名男同学,若规定男同学的跳绳成绩在120个以上(含120个)为合格,估计该校八年级男同学成绩合格的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,四边形
 各顶点的坐标分别为
各顶点的坐标分别为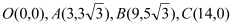 ,动点
,动点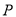 与
与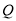 同时从
同时从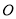 点出发,运动时间为
点出发,运动时间为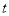 秒,点
秒,点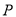 沿
沿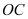 方向以
方向以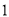 单位长度/秒的速度向点
单位长度/秒的速度向点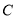 运动,点
运动,点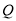 沿折线
沿折线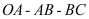 运动,在
运动,在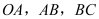 上运动的速度分别为
上运动的速度分别为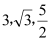 (单位长度/秒).当
(单位长度/秒).当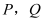 中的一点到达
中的一点到达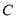 点时,两点同时停止运动.
点时,两点同时停止运动.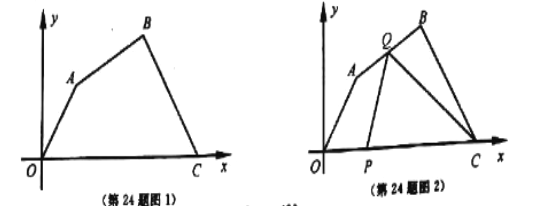
(1)求
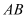 所在直线的函数表达式;
所在直线的函数表达式;(2)如图2,当点
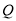 在
在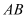 上运动时,求
上运动时,求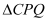 的面积
的面积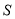 关于
关于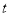 的函数表达式及
的函数表达式及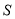 的最大值;
的最大值;(3)在
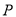 ,
,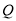 的运动过程中,若线段
的运动过程中,若线段 的垂直平分线经过四边形
的垂直平分线经过四边形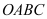 的顶点,求相应的
的顶点,求相应的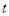 值.
值. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=﹣(x+1)2+8的开口方向是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=2x+3与y轴交于点A,直线y=kx﹣1与y轴交于点B,与直线y=2x+3交于点C(﹣1,n).
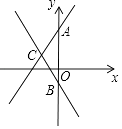
(1)求n、k的值;
(2)求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】与表示﹣2的点相距3个单位长度的点所表示的数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)感知:如图①,四边形ABCD、CEFG均为正方形.易知BE=DG.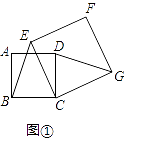
(2)探究:如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.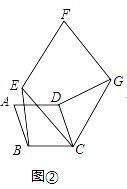
(3)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD的延长线上.若AE=3ED,∠A=∠F,△EBC的面积为8,则菱形CEFG的面积为 .
相关试题

