【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.

(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。

(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。

参考答案:
【答案】(1)①![]() ;②3(2)AM=
;②3(2)AM=![]() DE(3)
DE(3)![]()
【解析】
(1)①根据全等三角形的判定与性质推出△ABC与△DAE全等,再根据等腰直角三角形斜边上的高等于斜边的一半即可得出答案;②根据题意推出△ADE为等边三角形,推出AB的长度为6,即可得出AM (2) 过点A作AN⊥ED于N,证出∠DAN=![]() ∠DAE,ND =
∠DAE,ND =![]() DE和∠CAM=
DE和∠CAM=![]() ∠CAB,再证∠DAN+∠CAM=90°,∠DAN=∠C,推出
∠CAB,再证∠DAN+∠CAM=90°,∠DAN=∠C,推出
△AND≌△AMC,即可得出答案.
(1)①![]() ;②3
;②3
(2)猜想:结论AM=![]() DE.
DE.
证明:过点A作AN⊥ED于N
∵AE=AD,AN⊥ED
∴∠DAN=![]() ∠DAE,ND =
∠DAE,ND =![]() DE
DE

同理可得:∠CAM=![]() ∠CAB,
∠CAB,
∵∠DAE+∠CAB=180°,
∴∠DAN+∠CAM=90°,
∵∠CAM+∠C=90°
∴∠DAN=∠C,
∵AM⊥BC∴∠AMC=∠AND=90°
在△AND与△AMC中,
![]()
∴△AND≌△AMC,
∴ND=AM
∴AM=![]() DE.
DE.
(3)①图略;线段AC的中点或(线段AD的垂直平分线与线段AC的交点)或(线段BC的垂直平分线与线段AC的交点)等方法正确均可以给分;
②
PE为所求,由题意知,BC=![]() ,AB=
,AB=![]() ,
,
所以PE=![]() AB=
AB=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于实数a、b,定义一种运算“”为:ab=a2+ab﹣2,有下列命题: ①13=2;
②方程x1=0的根为:x1=﹣2,x2=1;
③不等式组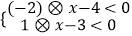 的解集为:﹣1<x<4;
的解集为:﹣1<x<4;
④点( ,
,  )在函数y=x(﹣1)的图象上.
)在函数y=x(﹣1)的图象上.
其中正确的是( )
A.①②③④
B.①③
C.①②③
D.③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:

(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足
 =
=  ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E=  ;④S△DEF=4
;④S△DEF=4  .
.
其中正确的是(写出所有正确结论的序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣2|+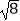 ﹣4sin45°﹣1﹣2
﹣4sin45°﹣1﹣2
(2)化简: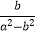
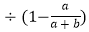 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.

(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
相关试题

