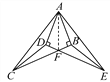
【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.

(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
参考答案:
【答案】(1)∠B′EC=2∠A′;(2)A′D′平分∠B′A′C.见解析
【解析】
试题分析:(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=![]() ∠BAC,即可得出∠B′A′D′=
∠BAC,即可得出∠B′A′D′=![]() ∠B′A′C.
∠B′A′C.
解:(1)∠B′EC=2∠A′,
理由:∵将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=![]() ∠BAC=
∠BAC=![]() ∠B′EC,
∠B′EC,
即∠B′EC=2∠A′;
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移至如图(2)所示,得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C,
∵∠BAD=![]() ∠BAC,
∠BAC,
∴∠B′A′D′=![]() ∠B′A′C,
∠B′A′C,
∴A′D′平分∠B′A′C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=∠ADE=90°,AD=AB,AC=AE,BC与DE相交于点F,连接CD、EB.
(1)图中共有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,比较适合用全面调查(普查)方式的是( ).
A.某灯具厂节能灯的使用寿命
B.全国居民年人均收入
C.某校今年初中生育体中考的成绩
D.全国快递包装产生的垃圾数量
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解决农民工子女就近入学问题,我市第一小学计划2012年秋季学期扩大办学规模.学校决定开支八万元全部用于购买课桌凳、办公桌椅和电脑,要求购买的课桌凳与办公桌椅的数量比为20:1,购买电脑的资金不低于16000元,但不超过24000元.已知一套办公桌椅比一套课桌凳贵80元,用2000元恰好可以买到10套课桌凳和4套办公桌椅.(课桌凳和办公桌椅均成套购进)
(1)一套课桌凳和一套办公桌椅的价格分别为多少元?
(2)求出课桌凳和办公桌椅的购买方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】一堆有红、白两种颜色的球若干个,已知白球的个数比红球少,但白球的2倍比红球多.若把每一个白球都记作“2”,每一个红球都记作“3”,则总数为“60”,那么这两种球各有多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);
(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;
(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).
相关试题

