【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论: ①△ADF∽△AED;②FG=2;③tan∠E= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() .
.
其中正确的是(写出所有正确结论的序号).
参考答案:
【答案】①②④
【解析】解:①∵AB是⊙O的直径,弦CD⊥AB, ∴ ![]() ,DG=CG,
,DG=CG,
∴∠ADF=∠AED,
∵∠FAD=∠DAE(公共角),
∴△ADF∽△AED;
故①正确;
②∵ ![]() =
= ![]() ,CF=2,
,CF=2,
∴FD=6,
∴CD=DF+CF=8,
∴CG=DG=4,
∴FG=CG﹣CF=2;
故②正确;
③∵AF=3,FG=2,
∴AG= ![]() =
= ![]() ,
,
∴在Rt△AGD中,tan∠ADG= ![]() =
= ![]() ,
,
∴tan∠E= ![]() ;
;
故③错误;
④∵DF=DG+FG=6,AD= ![]() =
= ![]() ,
,
∴S△ADF= ![]() DFAG=
DFAG= ![]() ×6×
×6× ![]() =3
=3 ![]() ,
,
∵△ADF∽△AED,
∴ ![]() =(
=( ![]() )2 ,
)2 ,
∴ ![]() =
= ![]() ,
,
∴S△AED=7 ![]() ,
,
∴S△DEF=S△AED﹣S△ADF=4 ![]() ;
;
故④正确.
所以答案是:①②④.
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若AG=13,CF=6,则四边形BDFG的周长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到(a+b)2=a2+2ab+b2,请解答下列问题:

(1)写出图2中所表示的数学等式 。
(2)根据整式乘法的运算法则,通过计算验证上述等式。
(3)利用(1)中得到的结论,解决下面的问题:
若a+b+c=10,ab+ac+bc=35,则a2+b2+c2= .
(4)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形z张边长分别为a、b的长方形纸片拼出一个面积为(5a+7b)(9a+4b)长方形,则x+y+z= 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.

(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。

(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=
 ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。

-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算:|﹣2|+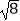 ﹣4sin45°﹣1﹣2
﹣4sin45°﹣1﹣2
(2)化简: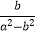
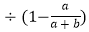 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC.

(1)猜想∠B′EC与∠A′之间的关系,并写出理由.
(2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,点A为线段BC外一动点,且BC=a,AB=b,填空:当点A位于 时,线段AC的长取到最大值,则最大值为 ;(用含a、b的式子表示)。
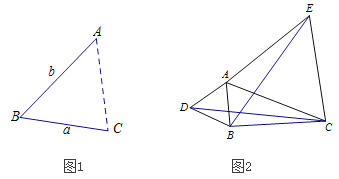
(2)如图2,若点A为线段BC外一动点,且BC=4,AB=2,分别以AB,AC为边,作等边
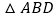 和等边
和等边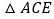 ,连接CD,BE.
,连接CD,BE. ①图中与线段BE相等的线段是线段 ,并说明理由;
②直接写出线段BE长的最大值为 。
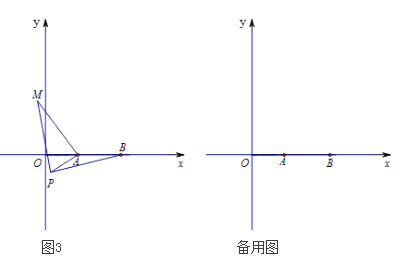
(3)如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值为 ,及此时点P的坐标为 。(提示:等腰直角三角形的三边长a、b、c满足a:b:c=1:1:
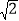 )
)
相关试题

