【题目】已知三条互相平行的直线a、b、c,请问能否作出一个等边△ABC,使其三个顶点A、B、C分别在直线a、b、c上?(用“能”或“不能”填空).若能,请说明作图方法;若不能,请简要说明理由. 
参考答案:
【答案】解:能, 如图,过点A作AD⊥b于D,再作AD′=AD,且∠D′AD=60°,
再作D′C⊥AD′交直线c于点C,以AC为半径,A点为圆心,
画弧交直线b于点B,△ABC即为所求.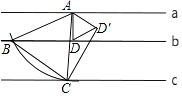
【解析】直接作AD′=AD,且∠D′AD=60°,进而作D′C⊥AD′交直线c于点C,进而得出答案.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补),还要掌握等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为2的等边三角形ABC绕点C旋转120°,得到△DCE,连接BD,则BD的长为( )
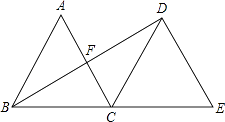
A.2
B.2.5
C.3
D.2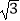
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样的规律摆下去,则第10(n是大于0的整数)个图形需要黑色棋子的个数是_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC中,AC=BC,∠ACB=90°,点O分斜边AB为BO:OA=1:
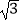 ,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= .
,将△BOC绕C点顺时针方向旋转到△AQC的位置,则∠AQC= . 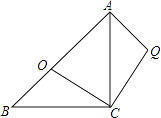
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:
 和
和 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即 =3+5;
=3+5; =7+9+11;
=7+9+11; =13+15+17+19;…;若
=13+15+17+19;…;若 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则 “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E,当P点在线段AD上运动时,∠E与∠B,∠ACB的数量关系为________________.
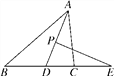
相关试题

