【题目】如图,在ABCD中,E是对角线BD上的一点,过点C作CF∥DB,且CF=DE,连接AE,BF,EF.
(1)求证:△ADE≌△BCF;
(2)若∠ABE+∠BFC=180°,则四边形ABFE是什么特殊四边形?说明理由.

参考答案:
【答案】(1)证明见解析;(2)四边形ABFE是菱形
【解析】
(1)根据平行四边形的性质和全等三角形的判定证明即可;
(2)根据平行四边形的性质和全等三角形的判定以及菱形的判定解答即可.
证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC.
∵CF∥DB,∴∠BCF=∠DBC,∴∠ADB=∠BCF
在△ADE与△BCF中
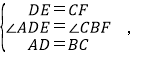 ∴△ADE≌△BCF(SAS).
∴△ADE≌△BCF(SAS).
(2)四边形ABFE是菱形
理由:∵CF∥DB,且CF=DE,∴四边形CFED是平行四边形,∴CD=EF,CD∥EF.
∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴AB=EF,AB∥EF,∴四边形ABFE是平行四边形.
∵△ADE≌△BCF,∴∠AED=∠BFC.
∵∠AED+∠AEB=180°,∴∠ABE=∠AEB,∴AB=AE,∴四边形ABFE是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用下列边长相同的正多边形组合,能够铺满地面不留缝隙的是()
A. 正八边形和正三角形 B. 正五边形和正八边形
C. 正六边形和正三角形 D. 正六边形和正五边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形
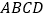 中,
中, 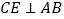 ,垂足为
,垂足为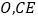 与
与 的延长线相交于
的延长线相交于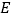 ,且
,且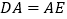 ,连接
,连接 ;
;(1)如图
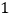 ,求证:四边形
,求证:四边形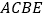 是菱形;
是菱形;(2)如图
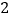 ,连接
,连接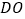 ,若
,若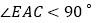 ,在不添加任何辅助线的情况下,直接写出图
,在不添加任何辅助线的情况下,直接写出图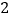 中所有面积等于
中所有面积等于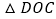 的面积的钝角三角形.
的面积的钝角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.

(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查,下面是根据收集的数据绘制的两幅不完整的统计图.

根据图中提供的信息,解答下列问题:
(1)此次共调查了名学生,扇形统计图中,“艺术鉴赏”所对应的圆心角的度数是度;
(2)请把这个条形统计图补充完整;
(3)现该校700名学生报名参加这四个选修项目,请你估计有多少名学生参加了“数学思维”项目. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC一腰上的中线BD把三角形的周长分成21cm和12cm两部分,求底边BC的长.

相关试题

