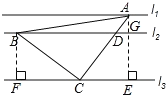
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上,AC交l2于D,∠ACB=90°.已知l1与l2的距离为2,l2与l3的距离为6,则![]() 的值为_____.
的值为_____.

参考答案:
【答案】![]()
【解析】如图,作BF⊥l3,AE⊥l3,
∵∠ACB=90°,
∴∠BCF+∠ACE=90°,
∵∠BCF+∠CFB=90°,
∴∠ACE=∠CBF,
在△ACE和△CBF中, 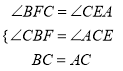 ,
,
∴△ACE≌△CBF,
∴CE=BF=6,CF=AE=8,
∵l1与l2的距离为2,l2与l3的距离为6,
∴AG=2,BG=EF=CF+CE=14,
∴AB=![]() ,
,
∵l2∥l3,
∴![]() ,
,
∴DG=![]() CE=
CE=![]() ,
,
∴BD=BG-DG=14-![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
故答案为: ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面图形,解答下列问题:

(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整:
边数
三
四
五
六
七
……
n
对角线
条数
0
2
5
……
(3)若一个多边形的内角和为 1440°,求这个多边形的边数和对角线的条数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形 ABC (顶点是网格线交点的三角形)的顶点 A ,C 的坐标分别是(-4 ,6) ,(-1,4) .
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC 关于 x 轴对称的△A1B1C1 ;并直接写出A1B1C1的坐标.
(3)请在 y 轴上求作一点 P ,使△PB1C 的周长最小,

-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年5月12日,汶川发生了里氏8.0级地震,给当地人民造成了巨大的损失.某中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:

老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:
信息一:这三个班的捐款总金额是7700元;
信息二:二班的捐款金额比三班的捐款金额多300元;
信息三:一班学生平均每人捐款的金额大于48元,小于51元.
请根据以上信息,帮助老师解决:
(1)二班与三班的捐款金额各是多少元?
(2)一班的学生人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求DE的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2,求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

相关试题

