【题目】如图1,已知点![]() 是线段
是线段![]() 上一点,点
上一点,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 上,
上,![]() 、
、![]() 两点分别从
两点分别从![]() 、
、![]() 出发以
出发以![]() 、
、![]() 的速度沿直线
的速度沿直线![]() 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.
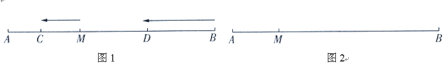
(1)若![]() ,当点
,当点![]() 、
、![]() 运动了
运动了![]() ,求
,求![]() 的值.
的值.
(2)若点![]() 、
、![]() 运动时,总有
运动时,总有![]() ,则:
,则:![]() ____________
____________![]() ,并说明理由.
,并说明理由.
(3)如图2,若![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)计算出CM及BD的长,进而可得出答案;
(2)根据题意可知BD+MD=3CM+3AC,即BM=3AM,依此即可求出AM的长;
(3)分两种情况讨论,①当点N在线段AB上时,②当点N在线段AB的延长线上时,然后根据数量关系即可求解.
解:(1)当点![]() 、
、![]() 运动了
运动了![]() 时,
时,![]() ,
,![]()
![]() ,
,![]()
![]()
![]() .
.
(2)![]() ,
,![]() 两点的速度分别为
两点的速度分别为![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() ,即
,即![]() ,
,
![]() ;
;
(3)当点![]() 在线段
在线段![]() 上时,如图
上时,如图
![]()
![]() ,
,
又![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
当点![]() 在线段
在线段![]() 的延长线上时,如图
的延长线上时,如图
![]()
![]() ,
,
又![]()
![]() ,即
,即![]() .
.
综上所述![]() 或
或![]() .
.
-
科目: 来源: 题型:
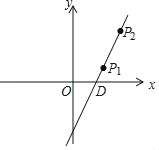
查看答案和解析>>【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
(1)点P2的坐标为 ;
(2)求直线l的解析表达式;
(3)求直线y=﹣x+b经过点P1,交x轴于点C,则b的值是多少?已知直线l与x轴交于点D,求△P1CD的面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的第一条边的长是
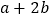 ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。(1)用含
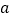 、
、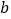 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;(2)当
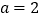 ,
,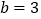 时,求这个三角形的周长;
时,求这个三角形的周长;(3)当
 ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上的一点,连接PA,PC.
(1)证明:∠PAB=∠PCB;
(2)在BC上截取一点E,连接PE,使得PE=PC,连接AE,判断△PAE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

-
科目: 来源: 题型:
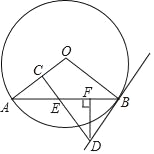
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,过D点作DF⊥AB于点F,
①则cos∠EDF= ;
②求⊙O的半径.
相关试题

