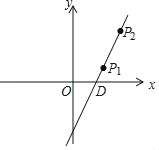
【题目】如图,直线l上有一点P1(2,1),将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P2恰好在直线l上.
(1)点P2的坐标为 ;
(2)求直线l的解析表达式;
(3)求直线y=﹣x+b经过点P1,交x轴于点C,则b的值是多少?已知直线l与x轴交于点D,求△P1CD的面积是多少?
参考答案:
【答案】(1)(3,3).(2)y=2x﹣3.(3)![]() .
.
【解析】分析:(1)根据“右加左减、上加下减”的规律来求点P2的坐标;
(2)设直线l所表示的一次函数的表达式为y=kx+b(k≠0),把点P1(2,1),P2(3,3)代入直线方程,利用方程组来求系数的值;
(3)根据点P1的坐标可求出b值,进而得出C、E的坐标,利用一次函数图象上点的坐标特征可求出点D的坐标,再根据三角形的面积公式结合![]() =S△COE﹣S△COD﹣
=S△COE﹣S△COD﹣![]() 即可求出△P1CD的面积.
即可求出△P1CD的面积.
详解:(1)∵将点P1先向右平移1个单位,再向上平移2个单位得到像点P2,点P1的坐标为(2,1),
∴点P2的坐标为(3,3).
故答案为:(3,3).
(2)设直线l的解析表达式为y=mx+n(m≠0),
将P1(2,1)、P2(3,3)代入y=mx+n,
得![]() ,解得:
,解得:![]() ,
,
∴直线l的解析表达式为y=2x﹣3.
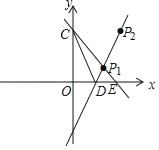
(3)∵求直线y=﹣x+b经过点P1(2,1),
∴1=﹣2+b,
∴b=3,
∴直线CP1的解析表达式为y=﹣x+3,
∴点C的坐标为(0,3).
设直线CP1的x轴的交点为E,则点E(3,0).
当y=0时,有2x﹣3=0,
解得:x=![]() ,
,
∴点D的坐标为(![]() ,0),
,0),
∴![]() =S△COE﹣S△COD﹣
=S△COE﹣S△COD﹣![]() =
=![]() ×3×3﹣
×3×3﹣![]() ×3×
×3×![]() ﹣
﹣![]() ×
×![]() ×1=
×1=![]() .
.
-
科目: 来源: 题型:
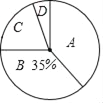
查看答案和解析>>【题目】2017年4月15日至5月15日,某市约8万名初三毕业生参加了中考体育测试,为了了解今年初三毕业生的体育成绩,从某校随机抽取了60名学生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
等级
成绩(分)
频数(人数)
频率
A
27~30
24
0.4
B
23~26
m
x
C
19~22
n
y
D
18及18以下
3
0.05
合计
60
1.00
请你根据以上图表提供的信息,解答下列问题:
(1)m= ,n= ,x= ,y= ;
(2)在扇形图中,B等级所对应的圆心角是 度;
(3)请你估计某市这8万名初三毕业生成绩等级达到优秀和良好的大约有多少人?
(4)初三(1)班的甲、乙、丙、丁四人的成绩均为A,现决定从这四名同学中选两名参加学校组织的体育活动,直接写出恰好选中甲、乙两位同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管和一个出水管的容器,每分钟的进水量和出水量都是常数.从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水.如图表示的是容器中的水量y(升)与时间t(分钟)的图象.
(1)当4≤t≤12时,求y关于t的函数解析式;
(2)当t为何值时,y=27?
(3)求每分钟进水、出水各是多少升?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②DE=DN.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的第一条边的长是
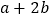 ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。(1)用含
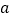 、
、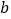 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;(2)当
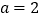 ,
,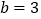 时,求这个三角形的周长;
时,求这个三角形的周长;(3)当
 ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD的对角线BD上的一点,连接PA,PC.
(1)证明:∠PAB=∠PCB;
(2)在BC上截取一点E,连接PE,使得PE=PC,连接AE,判断△PAE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点
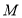 是线段
是线段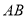 上一点,点
上一点,点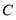 在线段
在线段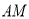 上,点
上,点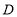 在线段
在线段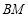 上,
上,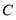 、
、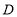 两点分别从
两点分别从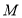 、
、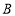 出发以
出发以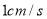 、
、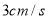 的速度沿直线
的速度沿直线 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.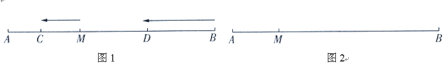
(1)若
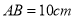 ,当点
,当点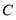 、
、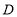 运动了
运动了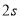 ,求
,求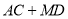 的值.
的值.(2)若点
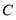 、
、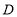 运动时,总有
运动时,总有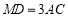 ,则:
,则: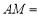 ____________
____________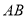 ,并说明理由.
,并说明理由.(3)如图2,若
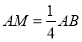 ,点
,点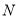 是直线
是直线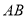 上一点,且
上一点,且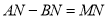 ,求
,求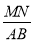 的值.
的值.
相关试题

