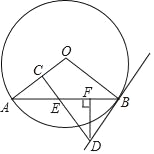
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,过D点作DF⊥AB于点F,
①则cos∠EDF= ;
②求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)①![]() ;②
;②![]()
【解析】分析:(1)欲证明DB=DE,只要证明∠DEB=∠DBE;
(2)①连接OE,有线段垂直平分线的性质,可得EF=BE=3,
在Rt△DEF中,由勾股定理DF=4,则cos∠EDF=![]() =
=![]() ;
;
②只要证明∠AOE=∠DEF,可得sin∠DEF=sin∠AOE=![]() ,由此求出AE即可解决问题.
,由此求出AE即可解决问题.
详解:(1)∵BD为切线,
∴OB⊥BD,
∴∠OBD=90°,即∠OBE+∠DBE=90°,
∵CD⊥OA,
∴∠A+∠AEC=90°,
而OA=OB,
∴∠A=∠OBE,
∴∠AEC=∠DBE,
∵∠AEC=∠DEB,
∴∠DEB=∠DBE,
∴DB=DE;
(2)①连接OE,如图,
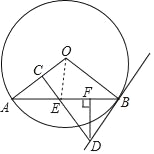
∵E是AB的中点,
∴AE=BE=6,
∵DE=DB=5,DF⊥BE,
∴EF=BE=3,
在Rt△DEF中,DF=![]() =4,
=4,
cos∠EDF=![]() =
=![]() ;
;
故答案为![]() ;
;
②连接OE,
∵E是AB的中点,
∴OE⊥AB,
∴∠OEB=90°
∴∠EOB+∠EBO=90°,
而∠OBE+∠DBE=90°,
∴∠EOB=∠DBF,
在Rt△OBE中,sin∠EOB=![]() =sin∠DBF=
=sin∠DBF=![]() ,
,
∴OB=![]() =
=![]() ,
,
即⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知点
 是线段
是线段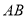 上一点,点
上一点,点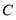 在线段
在线段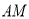 上,点
上,点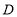 在线段
在线段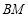 上,
上,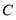 、
、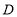 两点分别从
两点分别从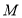 、
、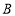 出发以
出发以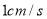 、
、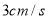 的速度沿直线
的速度沿直线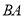 向左运动,运动方向如箭头所示.
向左运动,运动方向如箭头所示.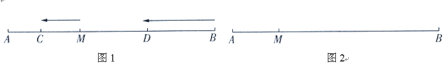
(1)若
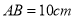 ,当点
,当点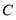 、
、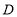 运动了
运动了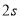 ,求
,求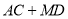 的值.
的值.(2)若点
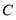 、
、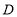 运动时,总有
运动时,总有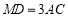 ,则:
,则: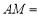 ____________
____________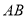 ,并说明理由.
,并说明理由.(3)如图2,若
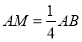 ,点
,点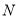 是直线
是直线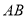 上一点,且
上一点,且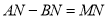 ,求
,求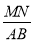 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】嫦娥四号探测器于2019年1月3日,成功着陆在月球背面,通过“鹊桥”中继星传回了世界第一张近距离拍摄的月背影像图,开启了人类月球探测新篇章.当中继星成功运行于地月拉格朗日L2点时,它距离地球约1500000km.用科学记数法表示数1500000为( )

A. 15×105 B. 1.5×106 C. 0.15×107 D. 1.5×105
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,-3),动点P在抛物线上.
(1)b =_________,c =_________,点B的坐标为_____________;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.

-
科目: 来源: 题型:
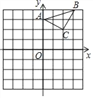
查看答案和解析>>【题目】已知:△ABC在坐标平面内,三个顶点的坐标分别为A(0,3),B(3,4),C(2,2).(正方形网格中,每个小正方形的边长是1个单位长度)
(1)画出△ABC向下平移4个单位,再向左平移1个单位得到的△A1B1C1,并直接写出C1点的坐标;
(2)作出△ABC绕点A顺时针方向旋转90°后得到的△A2B2C2,并直接写出C2点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在高速公路上的一个测速点,仪器记录下过往车辆的行驶速度(单位:千米/时),分析人员随机选取了10个速度数据如下:98,99,102,105,97,86,105,110,95,91.求这组数据的平均数、中位数和众数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
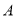 点的初始位置位于数轴上表示
点的初始位置位于数轴上表示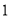 的点,现对
的点,现对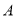 点做如下移动:第
点做如下移动:第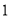 次向左移动
次向左移动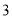 个单位长度至
个单位长度至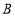 点,第
点,第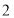 次从
次从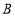 点向右移动
点向右移动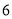 个单位长度至
个单位长度至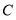 点,第
点,第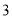 次从
次从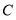 点向左移动
点向左移动 个单位长度至
个单位长度至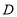 点,第
点,第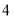 次从
次从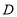 点向右移动
点向右移动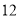 个单位长度至
个单位长度至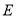 点,…,依此类推。这样第_____次移动到的点到原点的距离为
点,…,依此类推。这样第_____次移动到的点到原点的距离为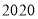 .
.
相关试题

