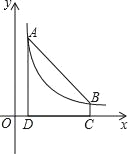
【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)(5,0)
(2)(5,0)
【解析】
(1)由反比例函数定义可知6m=n,m+5=n,联立可求解m和n的值,设反比例函数表达式为![]() ,代入A点坐标即可求解表达式;
,代入A点坐标即可求解表达式;
(2)设E(x,0),则DE=x﹣1,CE=6﹣x,则可分别计算或表示出S四边形ABCD、S△ADE、S△BCE的面积,再由S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE=5即可求解x的值.
(1)由题意得:![]() ,解得:
,解得:![]() ,
,
∴A(1,6),B(6,1),
设反比例函数表达式为![]() ,
,
将A(1,6)代入得:k=6,
则反比例表达式为y=![]() ;
;
(2)存在,
设E(x,0),则DE=x﹣1,CE=6﹣x,
∵AD⊥x轴,BC⊥x轴,
∴∠ADE=∠BCE=90°,
连结AE,BE,
则S△ABE=S四边形ABCD﹣S△ADE﹣S△BCE
=![]() (BC+AD)DC﹣
(BC+AD)DC﹣![]() DEAD﹣
DEAD﹣![]() CEBC
CEBC
=![]() ×(1+6)×5﹣
×(1+6)×5﹣![]() (x﹣1)×6﹣
(x﹣1)×6﹣![]() (6﹣x)×1
(6﹣x)×1
=![]() ﹣
﹣![]() x=5,
x=5,
解得:x=5,
则E(5,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数
0
1
2
3
4
5(含5次以上)
累计车费
0
0.5
0.9
a
b
1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数
0
1
2
3
4
5
人数
5
15
10
30
25
15
(Ⅰ)写出a,b的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数
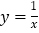 和
和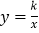 (k≠0)在第一象限内的图象如图所示,点P在
(k≠0)在第一象限内的图象如图所示,点P在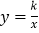 的图象上,PC⊥x轴,垂足为C,交
的图象上,PC⊥x轴,垂足为C,交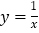 的图象于点A,PD⊥y轴,垂足为D,交
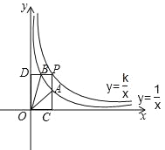
的图象于点A,PD⊥y轴,垂足为D,交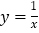 的图象于点B.已知点A(m,1)为线段PC的中点.
的图象于点B.已知点A(m,1)为线段PC的中点.(1)求m和k的值;
(2)求四边形OAPB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
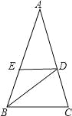
A. 1个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
-
科目: 来源: 题型:
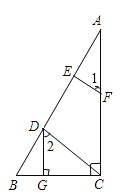
查看答案和解析>>【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
相关试题

