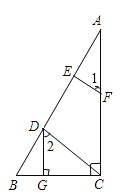
【题目】如图,已知DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB
参考答案:
【答案】见解析;
【解析】
灵活运用垂直的定义,注意由垂直可得90°角,由90°角可得垂直,结合平行线的判定和性质,只要证得∠ADC=90°,即可得CD⊥AB.
证明:∵ DG⊥BC,AC⊥BC(已知),
∴ ∠DGB=∠ACB=90°(垂直的定义),
∴ DG∥AC(同位角相等,两直线平行).
∴ ∠2=∠ACD(两直线平行,内错角相等).
∵ ∠1=∠2(已知),∴ ∠1=∠ACD(等量代换),
∴ EF∥CD(同位角相等,两直线平行).
∴ ∠AEF=∠ADC(两直线平行,同位角相等).
∵ EF⊥AB(已知),∴ ∠AEF=90°(垂直的定义),
∴ ∠ADC=90°(等量代换).
∴ CD⊥AB(垂直的定义).
-
科目: 来源: 题型:
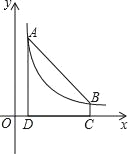
查看答案和解析>>【题目】如图,点A(m,6),B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连结AB,在线段DC上是否存在一点E,使△ABE的面积等于5?若存在,求出点E的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
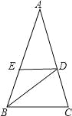
查看答案和解析>>【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
A. 1个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=
 ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,BD为对角线,点P从A出发,沿射线AB运动,连接PD,过点D作DE⊥PD,交直线BC于点E.
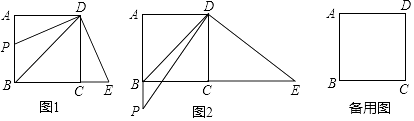
(1)探究发现:
当点P在线段AB上时(如图1),BP+CE=BD;
(2)数学思考:
当点P在线段AB的延长线上时(如图2),猜想线段BP、CE,BD之间满足的关系式,并加以证明;
(3)拓展应用:
若直线PE分别交线段BD、CD于点M、N,PM=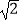 ,EN=
,EN= 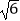 ,直接写出PD的长.
,直接写出PD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线a:y=2x﹣6,和直线b:y=﹣
 x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.
x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.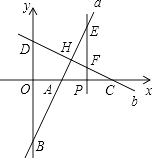
(1)求点H的坐标;
(2)判断直线a、b的位置关系,并说明理由;
(3)设点P的横坐标为m,当m为何值时,以D、E、F、O为顶点的四边形是
平行四边形,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?
相关试题

