【题目】如图,直线EF,CD相交于点0,OA⊥OB,且OC平分∠AOF,
(1)若∠AOE=40°,求∠BOD的度数;
(2)若∠AOE=α,求∠BOD的度数;(用含α的代数式表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

参考答案:
【答案】(1)20°;(2)![]() α;(3)∠AOE=2∠BOD.
α;(3)∠AOE=2∠BOD.
【解析】试题分析:(1)、(2)根据平角的性质求得∠AOF,又有角平分线的性质求得∠FOC;然后根据对顶角相等求得∠EOD=∠FOC;∠BOE=∠AOB﹣∠AOE,∠BOD=∠EOD﹣∠BOE;
(3)由(1)、(2)的结果找出它们之间的倍数关系.
试题解析:(1)∵∠AOE+∠AOF=180°(互为补角),∠AOE=40°,
∴∠AOF=140°;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=70°,
∠AOF=70°,
∴∠EOD=∠FOC=70°(对顶角相等);
而∠BOE=∠AOB﹣∠AOE=50°,
∴∠BOD=∠EOD﹣∠BOE=20°;
(2)∵∠AOE+∠AOF=180°(互为补角),∠AOE=α,
∴∠AOF=180°﹣α;
又∵OC平分∠AOF,
∴∠FOC=![]() ∠AOF=90°﹣
∠AOF=90°﹣![]() α,
α,
∴∠EOD=∠FOC=90°﹣![]() α(对顶角相等);
α(对顶角相等);
而∠BOE=∠AOB﹣∠AOE=90°﹣α,
∴∠BOD=∠EOD﹣∠BOE=![]() α;
α;
(3)从(1)(2)的结果中能看出∠AOE=2∠BOD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一等腰三角形两边长分别为3,4.则这个等腰三角形的周长为( )
A. 7 B. 11 C. 7或10 D. 10或11
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知9的算术平方根为a,b的绝对值为4,求a-b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:能够成为直角三角形三条边长的三个正整数
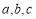 ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为:
,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: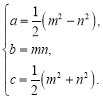 其中
其中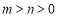 ,
, 是互质的奇数.
是互质的奇数.应用,当
 时,求有一边长为5的直角三角形的另外两条边长.
时,求有一边长为5的直角三角形的另外两条边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
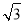 x﹣6分别交x轴,y轴于A,B,M是反比例函数y=
x﹣6分别交x轴,y轴于A,B,M是反比例函数y= (x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=4
(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=4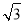 ,则k的值为( )
,则k的值为( )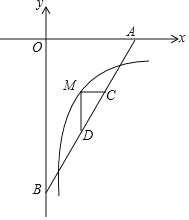
A.﹣3 B.﹣4 C.﹣5 D.﹣6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,10个不同的正偶数按下图排列,箭头上方的每个数都等于其下方两数的和,如
 ,
, 表示a1=a2+a3,则a1的最小值为( )
表示a1=a2+a3,则a1的最小值为( )
A.32 B.36 C.38 D.40
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列所学过的真命题中,是基本事实的是( )
A.两直线平行,内错角相等
B.同位角相等,两直线平行
C.三角形两边之和大于第三边
D.同角的余角相等
相关试题

