搜索
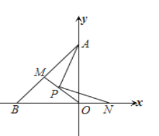
【题目】如图，在平面直角坐标系中，OA=OB，点P为△ABO的角平分线的交点，若PN⊥PA交x轴于N，延长OP交AB于M，写出AO，ON，PM之间的数量关系，并证明之．
参考答案：
【答案】AO-ON=2PM，证明见解析
【解析】
作 PE⊥x轴于E，PF⊥y轴于F，求出PF=PE，∠APF=∠NPE，根据ASA证△APF≌△NPE，推出AF=EN即可．
AO-ON=2PM，证明如下：
作 PE⊥x轴于E，PF⊥y轴于 F，则∠AFP=∠NEP=90°，
∵P是△AOB角平分线交点，∴PF=PE
∵PE⊥x轴，PF⊥y轴
∴∠PFO=∠PEO=∠FOE=90°，∴∠FPE=90°
∵AP⊥PN，
∴∠APN=90°=∠FPE
∴∠APN-∠FPN=∠FPE-∠FPN
即∠APF=∠NPE
在
与
中
∴
∴
∴AO-ON =（AF+OF）-（NE-OE）=2OE=2PF=2PM
即AO-ON=2PM．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，如图，已知Rt△DOE，∠DOE=90°，OD=3，点D在y轴上，点E在x轴上，在△ABC中，点A，C在x轴上，AC=5．∠ACB+∠ODE=180°，∠ABC=∠OED，BC=DE．按下列要求画图（保留作图痕迹）：
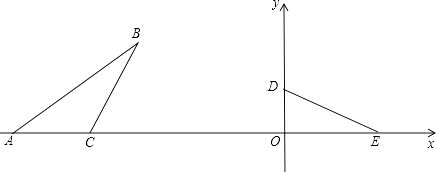
（1）将△ODE绕O点按逆时针方向旋转90°得到△OMN（其中点D的对应点为点M，点E的对应点为点N），画出△OMN；
（2）将△ABC沿x轴向右平移得到△A′B′C′（其中点A，B，C的对应点分别为点A′，B′，C′），使得B′C′与（1）中的△OMN的边NM重合；
（3）求OE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC中，AB=AC，∠BAC=90°．
（1）如图（1），CD平分∠ACB交AB于点D，BE⊥CD于点E，延长BE、CA相交于点F，请猜想线段BE与CD的数量关系，并说明理由．
（2）如图（2），点F在BC上，∠BFE=
∠ACB，BE⊥FE于点E，AB与FE交于点D，FH∥AC交AB于H，延长FH、BE相交于点G，求证：BE=FD；（3）如图（3），点F在BC延长线上，∠BFE=
∠ACB，BE⊥FE于点E，FE交BA延长线于点D，请你直接写出线段BE与FD的数量关系（不需要证明）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小商场以每件20元的价格购进一种服装，先试销一周，试销期间每天的销量（件）与每件的销售价x（元/件）如下表：
x（元/件）
38
36
34
32
30
28
26
t（件）
4
8
12
16
20
24
28
假定试销中每天的销售量t（件）与销售价x（元/件）之间满足一次函数．
（1）试求t与x之间的函数关系式；
（2）在商品不积压且不考虑其它因素的条件下，每件服装的销售定价为多少时，该小商场销售这种服装每天获得的毛利润最大？每天的最大毛利润是多少？（注：每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（－2，3），B（－5，0），C（－1，0），△ABC和△A1B1C1关于x轴对称．
（1）作△ABC关于x轴对称的△A1B1C1，直接写出点A1坐标；
（2）在y轴上有一点P使AP＋A1P最小，直接写出点P的坐标；
（3）请直接写出点A关于直线x=m（直线上各点的横坐标都为m）对称的点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：
（1）[﹣4.5]= ， ＜3.5＞= ．
（2）若[x]=2，则x的取值范围是；若＜y＞=﹣1，则y的取值范围是 ．
（3）已知x，y满足方程组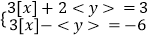
，求x，y的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，二次函数y=﹣
x2+ 
x+2的图象与x轴交于点A，B（点B在点A的左侧），与y轴交于点C．过动点H（0，m）作平行于x轴的直线l，直线l与二次函数y=﹣ x2+ x+2的图象相交于点D，E．
（1）写出点A，点B的坐标；
（2）若m＞0，以DE为直径作⊙Q，当⊙Q与x轴相切时，求m的值；
（3）直线l上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求m的值；若不存在，请说明理由．
相关试题
