【题目】我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3;用<a>表示大于a的最小整数,例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣4.5]= , <3.5>= .
(2)若[x]=2,则x的取值范围是;若<y>=﹣1,则y的取值范围是 .
(3)已知x,y满足方程组 ![]() ,求x,y的取值范围.
,求x,y的取值范围.
参考答案:
【答案】
(1)﹣5;4
(2)2≤x<3;﹣2≤y<﹣1
(3)解:解方程组得: ![]() ,
,
∴x,y的取值范围分别为﹣1≤x<0,2≤y<3.
【解析】解:(1)由题意得,[﹣4.5]=﹣5,<3.5>=4;
2)∵[x]=2,
∴x的取值范围是2≤x<3;
∵<y>=﹣1,
∴y的取值范围是﹣2≤y<﹣1;
(1)根据题目所给信息求解;(2)根据[2.5]=2,[3]=3,[﹣2.5]=﹣3,可得[x]=2中的2≤x<3,根据<a>表示大于a的最小整数,可得<y>=﹣1中,﹣2≤y<﹣1;(3)先求出[x]和<y>的值,然后求出x和y的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小商场以每件20元的价格购进一种服装,先试销一周,试销期间每天的销量(件)与每件的销售价x(元/件)如下表:
x(元/件)
38
36
34
32
30
28
26
t(件)
4
8
12
16
20
24
28
假定试销中每天的销售量t(件)与销售价x(元/件)之间满足一次函数.
(1)试求t与x之间的函数关系式;
(2)在商品不积压且不考虑其它因素的条件下,每件服装的销售定价为多少时,该小商场销售这种服装每天获得的毛利润最大?每天的最大毛利润是多少?(注:每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=OB,点P为△ABO的角平分线的交点,若PN⊥PA交x轴于N,延长OP交AB于M,写出AO,ON,PM之间的数量关系,并证明之.
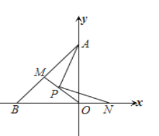
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(-2,3),B(-5,0),C(-1,0),△ABC和△A1B1C1关于x轴对称.
(1)作△ABC关于x轴对称的△A1B1C1,直接写出点A1坐标;
(2)在y轴上有一点P使AP+A1P最小,直接写出点P的坐标;
(3)请直接写出点A关于直线x=m(直线上各点的横坐标都为m)对称的点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,二次函数y=﹣
 x2+
x2+  x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣
x+2的图象与x轴交于点A,B(点B在点A的左侧),与y轴交于点C.过动点H(0,m)作平行于x轴的直线l,直线l与二次函数y=﹣  x2+
x2+  x+2的图象相交于点D,E.
x+2的图象相交于点D,E.
(1)写出点A,点B的坐标;
(2)若m>0,以DE为直径作⊙Q,当⊙Q与x轴相切时,求m的值;
(3)直线l上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求m的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=120°,DE垂直平分AC交BC于D,垂足为E,若DE=2cm,则BC的长为( )
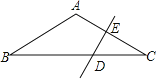
A. 6cm B. 8cm C. 10cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点M(
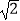 ,
, 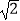 ),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是
),以点M为圆心,OM长为半径作⊙M.使⊙M与直线OM的另一交点为点B,与x轴,y轴的另一交点分别为点D,A(如图),连接AM.点P是 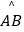 上的动点.
上的动点. 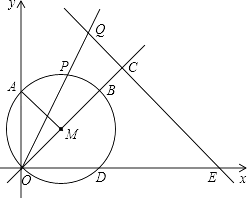
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OPOQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E. ①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S.求S与t的函数关系式及S的取值范围.
相关试题

