搜索
【题目】某小商场以每件20元的价格购进一种服装，先试销一周，试销期间每天的销量（件）与每件的销售价x（元/件）如下表：
x（元/件） | 38 | 36 | 34 | 32 | 30 | 28 | 26 |
t（件） | 4 | 8 | 12 | 16 | 20 | 24 | 28 |
假定试销中每天的销售量t（件）与销售价x（元/件）之间满足一次函数．
（1）试求t与x之间的函数关系式；
（2）在商品不积压且不考虑其它因素的条件下，每件服装的销售定价为多少时，该小商场销售这种服装每天获得的毛利润最大？每天的最大毛利润是多少？（注：每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价）
参考答案：
【答案】
（1）解：设t与x之间的函数关系式为：t=kx+b，因为函数的图象经过（38，4）和（36，8）两点，
∴ 
，
解得： 
．
故t=﹣2x+80．
（2）解：设每天的毛利润为W元，每件服装销售的毛利润为（x﹣20）元，每天售出（80﹣2x）件，
则W=（x﹣20）（80﹣2x）=﹣2x2+120x﹣1600=﹣2（x﹣30）2+200，
当x=30时，获得的毛利润最大，最大毛利润为200元．
【解析】（1）设y与x的函数关系式为t=kx+b，将x=38，y=4；x=36，y=8分别代入求出k、b，即可得到k与x之间的函数关系式；（2）根据利润=（售价﹣成本）×销售量列出函数关系式，利用二次函数的性质即可求出小商场销售这种服装每天获得的毛利润最大值以及每天的最大毛利润是多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一只不透明的箱子里共有3个球，把它们的分别编号为1，2，3，这些球除编号不同外其余都相同．
（1）从箱子中随机摸出一个球，求摸出的球是编号为1的球的概率；
（2）从箱子中随机摸出一个球，记录下编号后将它放回箱子，搅匀后再摸出一个球并记录下编号，求两次摸出的球都是编号为3的球的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，如图，已知Rt△DOE，∠DOE=90°，OD=3，点D在y轴上，点E在x轴上，在△ABC中，点A，C在x轴上，AC=5．∠ACB+∠ODE=180°，∠ABC=∠OED，BC=DE．按下列要求画图（保留作图痕迹）：
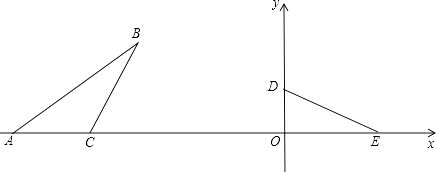
（1）将△ODE绕O点按逆时针方向旋转90°得到△OMN（其中点D的对应点为点M，点E的对应点为点N），画出△OMN；
（2）将△ABC沿x轴向右平移得到△A′B′C′（其中点A，B，C的对应点分别为点A′，B′，C′），使得B′C′与（1）中的△OMN的边NM重合；
（3）求OE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC中，AB=AC，∠BAC=90°．
（1）如图（1），CD平分∠ACB交AB于点D，BE⊥CD于点E，延长BE、CA相交于点F，请猜想线段BE与CD的数量关系，并说明理由．
（2）如图（2），点F在BC上，∠BFE=
∠ACB，BE⊥FE于点E，AB与FE交于点D，FH∥AC交AB于H，延长FH、BE相交于点G，求证：BE=FD；（3）如图（3），点F在BC延长线上，∠BFE=
∠ACB，BE⊥FE于点E，FE交BA延长线于点D，请你直接写出线段BE与FD的数量关系（不需要证明）．
-
科目： 来源： 题型：
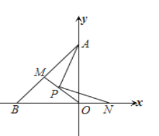
查看答案和解析>>【题目】如图，在平面直角坐标系中，OA=OB，点P为△ABO的角平分线的交点，若PN⊥PA交x轴于N，延长OP交AB于M，写出AO，ON，PM之间的数量关系，并证明之．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A（－2，3），B（－5，0），C（－1，0），△ABC和△A1B1C1关于x轴对称．
（1）作△ABC关于x轴对称的△A1B1C1，直接写出点A1坐标；
（2）在y轴上有一点P使AP＋A1P最小，直接写出点P的坐标；
（3）请直接写出点A关于直线x=m（直线上各点的横坐标都为m）对称的点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：
（1）[﹣4.5]= ， ＜3.5＞= ．
（2）若[x]=2，则x的取值范围是；若＜y＞=﹣1，则y的取值范围是 ．
（3）已知x，y满足方程组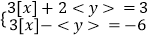
，求x，y的取值范围．
相关试题
