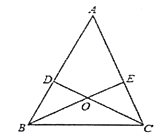
【题目】如图,已知AB=AC,AD=AE,BE与CD相交于O.图中全等的三角形有( )对.
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】
首先利用SAS定理证明△ADC≌△AEB,进而得到DC=EB,再证明△DBC≌△ECB,然后证明△DOB≌△EOC.
∵在△ADC和△AEB中,
 ,
,
∴△ADC≌△AEB(SAS),
∴DC=EB,
∵AB=AC,AD=AE,
∴DB=EC,

在△DBC和△ECB中,
 ,
,
∴△DBC≌△ECB(SSS),
∴∠DCB=∠EBC,
∵AB=AC,
∴∠ACB=∠ABC,
∴∠ACB-∠DCB=∠ABC-∠EBC,
即∠DBO=∠ECO,
在△DOB和△EOC中, ,
,
∴△DOB≌△EOC(AAS).
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
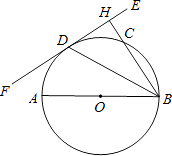
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(
 ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是
 ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y=
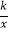 (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.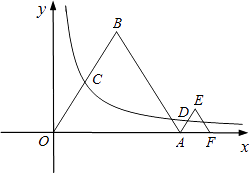
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=
 ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元? 
-
科目: 来源: 题型:
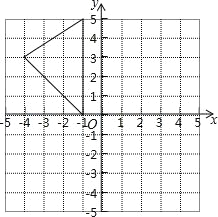
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果
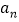 (
(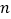 为正整数)表示这个数列的第
为正整数)表示这个数列的第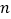 项,那么
项,那么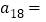 ,
,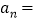 ;
;②如果欲求
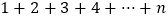 的值,可令
的值,可令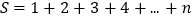 ……………①
……………①将①式右边顺序倒置,得
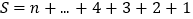 ……………②
……………②由②加上①式,得2
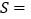 ;
; ∴ S=_________________;
由结论求
 ;
;(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果
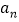 (
(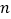 为正整数)表示这个数列的第
为正整数)表示这个数列的第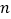 项,那么
项,那么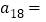 ,
,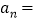 ;
;②为了求
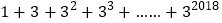 的值,可令
的值,可令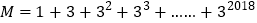 ,则
,则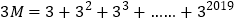 ,因此
,因此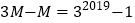 ,所以
,所以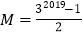 ,
,即
 .
. 仿照以上推理,计算
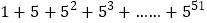
相关试题

