【题目】如图,等边△OAB和等边△AFE的一边都在x轴上,双曲线y= ![]() (k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.
(k>0)经过边OB的中点C和AE的中点D.已知等边△OAB的边长为4.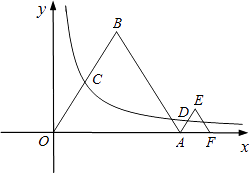
(1)求该双曲线所表示的函数解析式;
(2)求等边△AEF的边长.
参考答案:
【答案】
(1)
解:过点C作CG⊥OA于点G,
∵点C是等边△OAB的边OB的中点,
∴OC=2,∠AOB=60°,
∴OG=1,CG=OGtan60°=1 ![]() =
= ![]() ,
,
∴点C的坐标是(1, ![]() ),
),
由 ![]() =
= ![]() ,得:k=
,得:k= ![]() ,
,
∴该双曲线所表示的函数解析式为y= ![]()

(2)
解:过点D作DH⊥AF于点H,设AH=a,则DH= ![]() a.
a.

∴点D的坐标为(4+a, ![]() a),
a),
∵点D是双曲线y= ![]() 上的点,
上的点,
由xy= ![]() ,得
,得 ![]() a(4+a)=
a(4+a)= ![]() ,
,
即:a2+4a﹣1=0,
解得:a1= ![]() ﹣2,a2=﹣
﹣2,a2=﹣ ![]() ﹣2(舍去),
﹣2(舍去),
∴AD=2AH=2 ![]() ﹣4,
﹣4,
∴等边△AEF的边长是2AD=4 ![]() ﹣8
﹣8
【解析】(1)过点C作CG⊥OA于点G,根据等边三角形的性质求出OG、CG的长度,从而得到点C的坐标,再利用 待定系数法求反比例函数解析式列式计算即可得解;(2)过点D作DH⊥AF于点H,设AH=a,根据等边三角形的性质表示出DH的长度,然后表示出点D的坐标,再把点D的坐标代入反比例函数解析式,解方程得到a的值,从而得解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.
(1)求证:BD∥AC;
(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;
(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.
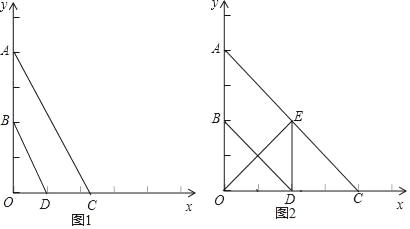
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
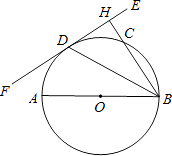
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(
 ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是
 ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AD=AE,BE与CD相交于O.图中全等的三角形有( )对.
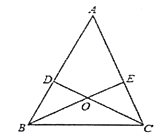
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=
 ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元? 
-
科目: 来源: 题型:
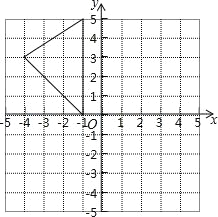
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
相关试题

