【题目】(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②如果欲求![]() 的值,可令
的值,可令
![]() ……………①
……………①
将①式右边顺序倒置,得![]() ……………②
……………②
由②加上①式,得2![]() ;
;
∴ S=_________________;
由结论求![]() ;
;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是 ;根据此规律,如果![]() (
(![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() ,
,![]() ;
;
②为了求![]() 的值,可令
的值,可令![]() ,则
,则![]() ,因此
,因此![]() ,所以
,所以![]() ,
,
即![]() .
.
仿照以上推理,计算![]()
参考答案:
【答案】(1)①1,18,n;②![]() ,
,![]() ,1540;(2)①2,
,1540;(2)①2,![]() ,
,![]() ;②
;②![]() .
.
【解析】
(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差都为1,从而可得常数为1;根据此规律,如果![]() 为正整数)=n,据此即可求得答案;
为正整数)=n,据此即可求得答案;
②观察可得2![]() n(n+1),从而求得 S;根据上面得到的式子进行计算即可求得
n(n+1),从而求得 S;根据上面得到的式子进行计算即可求得![]() 的值;
的值;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数2,根据此规律,可得![]() 为正整数)=2n,据此即可得答案;
为正整数)=2n,据此即可得答案;
②根据推理进行计算即可求得![]() 的值.
的值.
(1)①观察一列数1,2,3,4,5,…,发现从第二项开始,每一项与前一项之差是一个常数,这个常数是1;根据此规律,如果![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() 18,
18,![]() n,
n,
故答案为:1,18,n;
②令![]() ,①
,①
将①式右边顺序倒置,得![]() ,②
,②
②+①,得2![]()
![]() =n(1+n),
=n(1+n),
∴ S=![]() ;
;
![]() =
=![]() =1540,
=1540,
故答案为:![]() ,
,![]() ,1540;
,1540;
(2)①观察一列数2,4,8,16,32,…,发现从第二项开始,每一项与前一项之比是一个常数,这个常数是2;根据此规律,如果![]() 为正整数)表示这个数列的第
为正整数)表示这个数列的第![]() 项,那么
项,那么![]() 218,
218,![]() 2n,
2n,
故答案为:2,![]() ,
,![]() ;
;
②令![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AD=AE,BE与CD相交于O.图中全等的三角形有( )对.
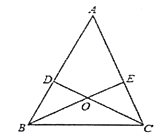
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明购买了一套安居型商品房,他准备将地面铺上地砖,地面结构如图所示.请根据图中的数据(单位:m),解答下列问题:
(1)用含x、y的代数式表示地面总面积;
(2)若x=5,y=
 ,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元?
,铺1m2地砖的平均费用为80元,那么铺地砖的总费用为多少元? 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(3)写出点A1,B1,C1的坐标.
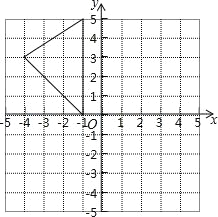
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加班长竞选,需进行演讲答辩与民主测评,民主测评时一人一票,按“优秀、良好、一般”三选一投票.如图是7位评委对小明“演讲答辩”的评分统计图及全班50位同学民主测评票数统计图.
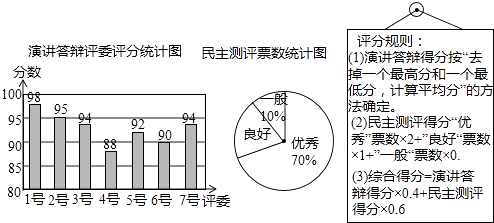
(1)求评委给小明演讲答辩分数的众数,以及民主测评为“良好”票数的扇形圆心角度数;
(2)求小明的综合得分是多少?
(3)在竞选中,小亮的民主测评得分为82分,如果他的综合得分不小于小明的综合得分,他的演讲答辩得分至少要多少分? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,点A是抛物线y=x2在第二象限上的点,连接OA,过点O作OB⊥OA,交抛物线于点B,以OA、OB为边构造矩形AOBC.

(1)如图1,当点A的横坐标为时,矩形AOBC是正方形;
(2)如图2,当点A的横坐标为- 时,
时,
①求点B的坐标;
②将抛物线y=x2作关于x轴的轴对称变换得到抛物线y=﹣x2 , 试判断抛物线y=﹣x2经过平移交换后,能否经过A,B,C三点?如果可以,说出变换的过程;如果不可以,请说明理由.
相关试题

