【题目】如图,已知AM//BN,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于
于![]() 、
、![]() .
.
(1)求![]() 的度数;
的度数;
(2)在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数是 ,并说明理由.

参考答案:
【答案】(1)∠CBD=60°;(2)不变化,∠APB=2∠ADB,证明见详解;(3)30°.
【解析】
(1)根据∠A=60°,则∠ABN=120°,由BC、BD分别平分∠ABP和∠PBN,即可得出![]() 的度数;
的度数;
(2)根据平行线的性质得出∠APB=∠PBN,∠ADB=∠DBN,再根据BD平分∠PBN,即可得到∠PBN=2∠DBN进而得出∠APB=2∠ADB;
(3)根据∠ACB=∠CBN,∠ACB=∠ABD,得出∠CBN=∠ABD,进而得到∠ABC=∠DBN,根据∠CBD=60°,∠ABN=120°,可求得∠ABC的度数.
解:(1)∵AM//BN,![]() ,
,
∴∠ABN=120°,
∴∠ABP+∠NBP=120°
∵![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)不变化,∠APB=2∠ADB,
证明:∵AM∥BN,
∴∠APB=∠PBN,
∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB=2∠ADB;
(3)∵AD∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠DBN,
由(1)可得,∠CBD=60°,∠ABN=120°,
∴∠ABC=![]() (120°
(120°![]() 60°)=30°.
60°)=30°.
故答案为:30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】安庆市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益,2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(每亩产出-每亩投入=每亩纯收入)
种类
投入(元)
产出(元)
马铃薯
1000
4500
蔬菜
1200
5300
(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?
(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?
-
科目: 来源: 题型:
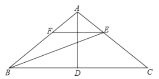
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.

(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH=( )

A.
B.
C.12
D.24 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,∠C=50°,AH,BD分别是△ABC高和角平分线,点P为边BC上一个点,当△BDP为直角三角形时,则∠CDP=_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:
①abc>0;②b<a+c;③4ac﹣b2>0;④2a+b=0
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
相关试题

