Question

【题目】如图，在Rt△ABC中，∠BAC＝90°，∠C＝50°，AH，BD分别是△ABC高和角平分线，点P为边BC上一个点，当△BDP为直角三角形时，则∠CDP＝_____度．

Answer 1

【答案】40或20．

【解析】

直接根据三角形内角和定理得∠ABC＝40°，由角平分线的定义得∠DBC＝20°，当△BDP为直角三角形时，存在两种情况：分别根据三角形外角的性质即可得出结论．

解：∵∠BAC＝90°，∠C＝50°，

∴∠ABC＝90°﹣50°＝40°

∵BD平分∠ABC

∴∠DBC＝＝20°

当△BDP为直角三角形时，有以下两种情况：

①当∠BPD＝90°时，如图1，

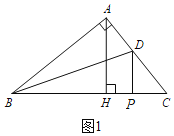
∵∠C＝90°，

∴∠CDP＝90°﹣50°＝40°；

②当∠BDP＝90°时，如图2，

∴∠BPD＝90°﹣20°＝70°，

∵∠BPD＝∠C+∠CDP，

∴∠CDP＝70°﹣50°＝20°，

综上，∠CDP的度数为40°或20°．

故答案为：40或20．