【题目】安庆市在精准扶贫活动中,因地制宜指导农民调整种植结构,增加种植效益,2018年李大伯家在工作队的帮助下,计划种植马铃薯和蔬菜共15亩,预计每亩的投入与产出如下表:(每亩产出-每亩投入=每亩纯收入)
种类 | 投入(元) | 产出(元) |
马铃薯 | 1000 | 4500 |
蔬菜 | 1200 | 5300 |
(1)如果这15亩地的纯收入要达到54900元,需种植马铃薯和蔬菜各多少亩?
(2)如果总投入不超过16000元,则最多种植蔬菜多少亩?该情况下15亩地的纯收入是多少?
参考答案:
【答案】(1)需种植马铃薯11亩,需种植蔬菜4亩;(2)最多种植蔬菜5亩,该情况下15亩地的纯收入是55500元.
【解析】
(1)设需种植马铃薯x亩,需种植蔬菜y亩,根据等量关系:一共15亩地;这15亩地的纯收入要达到54900元;列出关于x和y的二元一次方程组,解出即可;
(2)设种植马铃薯a亩,则需种植蔬菜(15-a)亩,根据“总投入不超过16000元”,列出关于a的一元一次不等式,解出即可.
(1)设需种植马铃薯![]() 亩,需种植蔬菜
亩,需种植蔬菜![]() 亩,依题意有
亩,依题意有
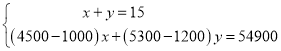 ,
,
解得![]() .
.
故需种植马铃薯11亩,需种植蔬菜4亩;
(2)设种植马铃薯![]() 亩,则需种植蔬菜
亩,则需种植蔬菜![]() 亩,依题意有
亩,依题意有
![]() ,
,
解得![]() ,
,
![]() (亩),
(亩),
![]()
![]()
![]() (元).
(元).
答:最多种植蔬菜5亩,该情况下15亩地的纯收入是55500元.
-
科目: 来源: 题型:
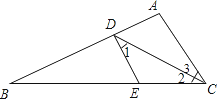
查看答案和解析>>【题目】如图,已知CD平分∠ACB,∠1=∠2.
(1)求证:DE∥AC;
(2)若∠3=30°,∠B=25°,求∠BDE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2
 ),点B在x轴的正半轴上,点E为线段AD的中点.
),点B在x轴的正半轴上,点E为线段AD的中点.
(1)如图1,求∠DAO的大小及线段DE的长;
(2)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3 .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可). -
科目: 来源: 题型:
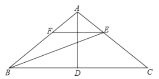
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.

(1)求A,B,C三点的坐标;
(2)若点P为线段BC上一点(不与B,C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当△BCM的面积最大时,在抛物线的对称轴上存在一点Q,使得△CNQ为直角三角形,求点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM//BN,
 ,点
,点 是射线
是射线 上一动点(与点
上一动点(与点 不重合),
不重合), 、
、 分别平分
分别平分 和
和 ,分别交射线
,分别交射线 于
于 、
、 .
.(1)求
 的度数;
的度数;(2)在点P的运动过程中,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数是 ,并说明理由.

相关试题

