【题目】已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE=α,直线AE与BD交于点F.
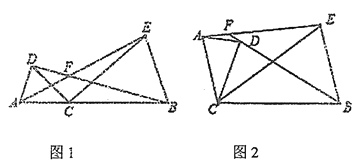
(1)如图1所示,
①求证AE= BD
②求∠AFB (用含α的代数式表示)
(2)将图1中的△ACD绕点C顺时针旋转某个角度(交点F至少在BD、AE中的一条线段上),得到如图2所示的图形,若∠AFB= 150°,请直接写出此时对应的α的大小(不用证明)
参考答案:
【答案】(1)①见解析,②180° -α(2)30°
【解析】
(1)①由∠ACD=∠BCE=α,得到∠ACE=∠DCB=180°![]() ,然后得到△ACE≌DCB,即可得到AE=BD;
,然后得到△ACE≌DCB,即可得到AE=BD;
②由①知△ACE≌DCB,则∠CAF=∠CDF,利用三角形内角和定理,由∠CAF+∠AFB+∠B=180°,∠CDF+∠DCB+∠B=180°,则∠AFB=∠DCB=![]() ;
;
(2)由∠AFB= 150°,则∠EFB=![]() ,由∠ACD=∠BCE,得∠ACE=∠DCB,然后得到△ACE≌△DCB,得到∠AEC=∠DBC,则∠BCE=∠EFB=30°.
,由∠ACD=∠BCE,得∠ACE=∠DCB,然后得到△ACE≌△DCB,得到∠AEC=∠DBC,则∠BCE=∠EFB=30°.
解:(1)如图1:
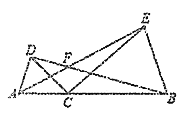
①证明:∵∠ACD=∠BCE=α,
∴180°![]() ∠ACD=180°
∠ACD=180°![]() ∠BCE,
∠BCE,
即∠ACE=∠DCB=180°![]() ,
,
∵CA=CD,CB=CE,
∴△ACE≌DCB,
∴AE=DB;
②∵△ACE≌DCB,
∴∠CAF=∠CDF,
由三角形内角和定理,得
∠CAF+∠AFB+∠B=180°,∠CDF+∠DCB+∠B=180°,
∴∠AFB=∠DCB=![]() ;
;
(2)如图2:
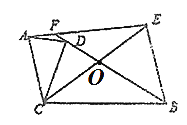
∵∠AFB= 150°,
∴∠EFB=![]() ,
,
∵∠ACD=∠BCE,
∴∠ACD+∠DCO=∠BCE+∠DCO,
∴∠ACE=∠DCB,
∵AC=DC,CE=CB,
∴△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠FOE=∠COB,
∴∠BCE=∠EFB=30°,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数
 的图象与
的图象与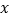 轴有两个交点,坐标分别为
轴有两个交点,坐标分别为 、
、 ,且
,且 ,图象上有一点
,图象上有一点 在
在 轴下方,在下列四个算式中判定正确的是________.
轴下方,在下列四个算式中判定正确的是________.①
 ;②
;② ;③
;③ ;④
;④ .
. -
科目: 来源: 题型:
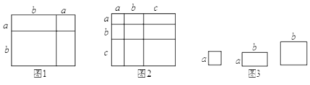
查看答案和解析>>【题目】(知识生成)我们已经知道,对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式,例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2请解答下列问题:
(1)写出图2中所表示的数学等式________________;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)小明同学用图3中x张边长为a的正方形,y张边长为b的正方形,z张宽、长分别为a,b的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=_______;
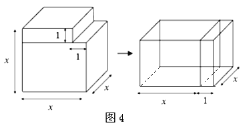
(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个数学等式:_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p
 q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p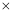 q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=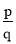 ,例如12可以分解为1
,例如12可以分解为1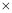 12,2
12,2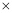 6或3
6或3 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=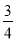 。
。(1)如果一个正整数
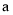 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB的垂直平分线分别交AB,BC于D,E,AC的垂直平分线分别交AC,BC于F,G.
(1)若△AEG的周长为10,求线段BC的长.
(2)若∠BAC=128°,求∠EAG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某活动小组为了估计装有
 个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共
个白球和若干个红球(每个球除颜色外都相同)的袋中红球接近多少个,在不将袋中球倒出来的情况下,分小组进行摸球试验,两人一组,共 组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做
组进行摸球实验.其中一位学生摸球,另一位学生记录所摸球的颜色,并将球放回袋中摇匀,每一组做 次试验,汇总起来后,摸到红球次数为
次试验,汇总起来后,摸到红球次数为 次.
次. 估计从袋中任意摸出一个球,恰好是红球的概率是多少?
估计从袋中任意摸出一个球,恰好是红球的概率是多少? 请你估计袋中红球接近多少个?
请你估计袋中红球接近多少个? -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场有
 、
、 两种商品,
两种商品, 商品每件售价
商品每件售价 元,
元, 商品每件售价
商品每件售价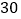 元,
元, 商品每件的成本是
商品每件的成本是 元.
元.根据市场调查“若按上述售价销售,该商场每天可以销售
 商品
商品 件,若销售单价毎上涨
件,若销售单价毎上涨 元,
元, 商品每天的销售量就减少
商品每天的销售量就减少 件.
件. 请写出
请写出 商品每天的销售利润
商品每天的销售利润 (元)与销售单价
(元)与销售单价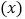 元之间的函数关系?
元之间的函数关系? 当销售单价为多少元时,
当销售单价为多少元时, 商品每天的销售利润最大,最大利润是多少?
商品每天的销售利润最大,最大利润是多少?
相关试题

