【题目】我们知道,对任意一个正整数n都可以进行这样的分解:n=p![]() q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p
q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p![]() q是n的最佳分解,并规定:F(n)=
q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解为1
,例如12可以分解为1![]() 12,2
12,2![]() 6或3
6或3![]() 4,因为12-1>6-2>4-3,所以3
4,因为12-1>6-2>4-3,所以3![]() 4是最佳分解,所以F(n)=
4是最佳分解,所以F(n)=![]() 。
。
(1)如果一个正整数![]() 是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1
(2)如果一个两位正整数t,t=10x+y (1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们就称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值。
参考答案:
【答案】(1)见解析;(2)F(t)的最大值为![]()
【解析】试题分析:(1)根据题意可设![]() 由最佳分解定义可得
由最佳分解定义可得![]()
(2)根据“吉祥数”定义知(10y+x)(10x+y)=9(yx)=18,即y=x+2,结合![]() 的范围可得2位数的“吉祥数”,求出每个“吉祥数”
的范围可得2位数的“吉祥数”,求出每个“吉祥数”![]() 的值.即可求出最大值.
的值.即可求出最大值.
试题解析:(1)对任意一个完全平方数m,设![]() (n为正整数),
(n为正整数),
∵|nn|=0,
∴n×n是m的最佳分解,
∴对任意一个完全平方数m, ![]()
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,
∵t为“吉祥数”,
∴t′t=(10y+x)(10x+y)=9(yx)=18,
∴y=x+2,
∵![]() x,y为自然数,
x,y为自然数,
∴“吉祥数”有:13,24,35,46,57,68,79,
∴所有“吉祥数”中F(t)的值为: ![]()
![]() 的最大值为
的最大值为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示).
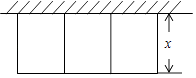
(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B的坐标分别为(0,8),(﹣3,0),点P从点A出发,以2单位/秒的速度沿射线AO方向运动,同时点E从点B出发,以1单位/秒的速度沿射线BO方向运动,以PE为斜边构造Rt△PEC(字母按逆时针顺序),且EC=2PC,抛物线y=﹣2x2+bx+c经过点(0,4),(﹣1,﹣2),设运动时间为t秒.
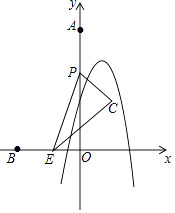
(1)求该抛物线的表达式;
(2)当t=2时,求点C的坐标;
(3)①当t<3时,求点C的坐标(用含t的代数式表示);
②在运动过程中,若点C恰好落在该抛物线上,请直接写出所有满足条件的t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形ABCD中,P是CD的中点,连接AP并延长,交BC的延长线于点F,作△CPF的外接圆⊙O,连接BP并延长交⊙O于点E,连接EF,则EF的长为( )

A.
B.
C.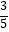

D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的解题过程:
计算:5÷(
 -2
-2 -2)×6.
-2)×6.解:5÷(
 -2
-2 -2)×6
-2)×6=5÷(-
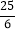 )×6…………①
)×6…………①=5÷(-25)…………②
=-
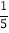 .…………③
.…………③回答:(1)上面的解题过程是从第________步开始出现错误的,错误的原因是___________________________________________________;
(2)请你给出正确的解题过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)
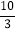 +(
+(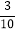 -
-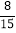 )÷(-
)÷(-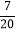 ); (2)-1-(1-
); (2)-1-(1- )÷3×|3-9|;
)÷3×|3-9|;(3)1
 +(2.4×
+(2.4× -
-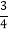 ×
× )÷2
)÷2 ; (4)(-3-1
; (4)(-3-1 )÷[3
)÷[3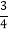 ÷(2-3
÷(2-3 )×1
)×1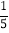 ].
]. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为线段AD上一点,B为CD的中点,且AD=10cm,BD=4cm;
(1)图中共有多少条线段?写出这些线段;
(2)求AC的长;
(3)若点E在直线AD上,且AE=3cm,求BE的长;

相关试题

