【题目】完成下面的证明.(在括号中注明理由)
已知:如图,BE∥CD,∠A=∠1,
求证:∠C=∠E.
证明:∵BE∥CD,(已知)
∴∠2=∠C,( )
又∵∠A=∠1,(已知)
∴AC∥ ,( )
∴∠2= ,( )
∴∠C=∠E(等量代换)

参考答案:
【答案】两直线平行,同位角相等;DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等
【解析】
首先根据平行线的性质求出∠2=∠C,进而求出AC∥DE,即可得到∠2=∠E,利用等量代换得到结论.
证明:∵BE∥CD,(已知)
∴∠2=∠C,(两直线平行,同位角相等)
又∵∠A=∠1,(已知)
∴AC∥DE,(内错角相等,两直线平行)
∴∠2=∠E,(两直线平行,内错角相等)
∴∠C=∠E(等量代换).
故答案为两直线平行,同位角相等;DE;内错角相等,两直线平行;∠E;两直线平行,内错角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点
 在
在 轴正半轴,点
轴正半轴,点 在
在 轴负半轴,连接
轴负半轴,连接 ,
, ,
,
(1)求点
 坐标
坐标(2)如图2,点
 是线段
是线段 上一点,连接
上一点,连接 ,以
,以 为直角边做等腰直角
为直角边做等腰直角 ,
, ,设点
,设点 的横坐标为
的横坐标为 ,求点
,求点 的坐标(用含
的坐标(用含 的代数式表示)
的代数式表示)(3)在(2)的条件下,如图3,在
 延长线上有一点
延长线上有一点 ,过点
,过点 作
作 的平行线,交
的平行线,交 轴于点
轴于点 ,延长
,延长 交
交 于点
于点 ,若
,若 ,
, ,求点
,求点 的坐标.
的坐标.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 为圆心的⊙P经过(-2, 0)以1个单位/秒的速度沿
为圆心的⊙P经过(-2, 0)以1个单位/秒的速度沿  轴向右运动,则当
轴向右运动,则当  与
与  轴相交的弦长为4时,则移动的时间为( )
轴相交的弦长为4时,则移动的时间为( )
A.2秒
B.3秒
C.2秒或4秒
D.3秒或6秒[来 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)写出点A、B的坐标:A( , )、B( , );
(2)求△ABC的面积;
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′,画出△A′B′C′,写出A′、B′、C′三个点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用标杆
 测量建筑物的高度,标杆
测量建筑物的高度,标杆  高
高  ,测得
,测得 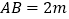 ,
,  ,则楼高
,则楼高  为=
为=  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O与直线
 相离,圆心
相离,圆心  到直线
到直线  的距离
的距离  ,
,  ,将直线
,将直线  绕点
绕点  逆时针旋转
逆时针旋转  后得到的直线
后得到的直线  刚好与⊙O相切于点
刚好与⊙O相切于点  ,则⊙O的半径= .
,则⊙O的半径= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
相关试题

