【题目】如图,在ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°

(1)求∠BAC的度数;
(2)若BD=2,求CD的长.
参考答案:
【答案】(1)75°;(2)2![]()
【解析】
(1)直接根据三角形内角和定理即可求出∠BAC的度数;
(2)先利用直角三角形的性质求出AB,再根据勾股定理得到AD,然后根据∠C=45°即可得出结论.
解:(1)∵在△ABC中,∠B=60°,∠C=45°,
∴∠BAC=180°-60°-45°=75°;
(2)∵AD⊥BC,
∴∠ADB=90°,△BDC是直角三角形,
又∵∠B=60°,
∴∠BAD=30°
∴AB=2BD=4
BD2 +AD2=AB2
∴AD=2![]()
又∵∠C=45°, ∠ADC=90°,
∴CD=AD=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
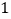 ,已知抛物线
,已知抛物线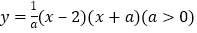 与
与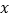 轴从左至右交于
轴从左至右交于 ,
,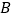 两点,与
两点,与 轴交于点
轴交于点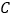 .
.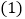 若抛物线过点
若抛物线过点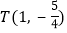 ,求抛物线的解析式;
,求抛物线的解析式;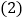 在第二象限内的抛物线上是否存在点
在第二象限内的抛物线上是否存在点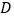 ,使得以
,使得以 、
、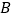 、
、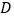 三点为顶点的三角形与
三点为顶点的三角形与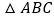 相似?若存在,求
相似?若存在,求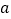 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.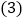 如图
如图 ,在
,在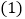 的条件下,点
的条件下,点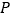 的坐标为
的坐标为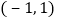 ,点
,点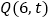 是抛物线上的点,在
是抛物线上的点,在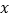 轴上,从左至右有
轴上,从左至右有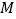 、
、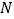 两点,且
两点,且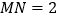 ,问
,问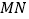 在
在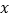 轴上移动到何处时,四边形
轴上移动到何处时,四边形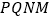 的周长最小?请直接写出符合条件的点
的周长最小?请直接写出符合条件的点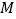 的坐标.
的坐标.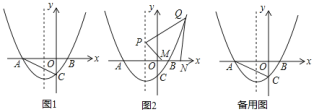
-
科目: 来源: 题型:
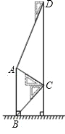
查看答案和解析>>【题目】如图,某中学在教学楼前新建了一座雕塑
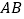 .为了测量雕塑的高度,小明在二楼找到一点
.为了测量雕塑的高度,小明在二楼找到一点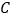 ,利用三角尺测得雕塑顶端点
,利用三角尺测得雕塑顶端点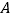 的仰角为
的仰角为 ,底部点
,底部点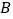 的俯角为
的俯角为 ,小华在五楼找到一点
,小华在五楼找到一点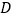 ,利用三角尺测得点
,利用三角尺测得点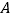 的俯角为
的俯角为 .若
.若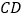 为
为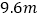 ,则雕塑
,则雕塑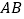 的高度为________
的高度为________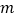 .(结果精确到
.(结果精确到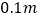 ,参考数据:
,参考数据: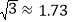 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】用硬纸板剪一个平行四边形ABCD,作出它的对角线的交点O,我们可以做如下操作:
用大头针把一根平放在平行四边形上的直细木条固定在点O处,并使细木条可以绕点O转动,拨动细木条,它可以停留在任意位置. 如果设细木条与一组对边AB,CD的交点分别为点E,F,则下列结论:①OE=OF;②AE=CF;③BE=DF;④△AOE≌△COF,其中一定成立的是_________________________(填写序号即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】请用两种不同的方法,在下图所给的两个矩形中各画一个不为正方形的菱形,且菱形的四个顶点都在矩形的边上(尺规作图,保留作图痕迹),并说明思路.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC中,D、E分别是AB、AC的中点,延长BC至点F,使CF =
 BC,连接DE、CD、EF.
BC,连接DE、CD、EF.
(1)求证:四边形DCFE是平行四边形;
(2)若等边三角形ABC的边长为a,写出求EF长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
(1)求证:CM=CN;
(2)若△CMN的面积与△CDN的面积比为3:1,且CD=4,求线段MN的长.

相关试题

