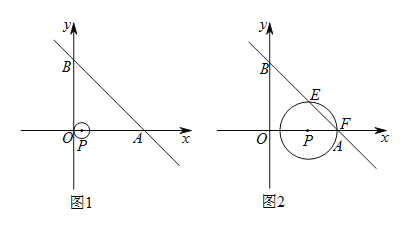
【题目】如图![]() ,一次函数
,一次函数![]() 的图像交
的图像交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() .以
.以![]() 为圆心的⊙
为圆心的⊙![]() 与
与![]() 轴相切,若点
轴相切,若点![]() 以每秒
以每秒![]() 个单位的速度沿
个单位的速度沿![]() 轴向右平移,同时⊙
轴向右平移,同时⊙![]() 的半径以每秒增加
的半径以每秒增加![]() 个单位的速度不断变大,设运动时间为
个单位的速度不断变大,设运动时间为![]() .
.
(![]() )点
)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________,
的坐标为__________,![]() __________
__________![]() .
.
(![]() )在运动过程中,点
)在运动过程中,点![]() 的坐标为__________,⊙
的坐标为__________,⊙![]() 的半径为__________(用含
的半径为__________(用含![]() 的代数式表示).
的代数式表示).
(![]() )当⊙
)当⊙![]() 与直线
与直线![]() 相交于点
相交于点![]() 、
、![]() 时.
时.
①如图![]() ,求
,求![]() 时弦
时弦![]() 的长.
的长.
②在运动过程中,是否存在以点![]() 为直角顶点的
为直角顶点的![]() ,若存在,请求出
,若存在,请求出![]() 的值;若不存在,请说明理由(利用图
的值;若不存在,请说明理由(利用图![]() 解题).
解题).
参考答案:
【答案】(1)(10,0),(0,10),45;(2)(1+2t,0),1+t;(3)①![]() ;②
;②![]() 或t=10.
或t=10.
【解析】试题分析:(1)利用待定系数法求出点A、B的坐标,即可解决问题.
(2)根据题意可得P(1+2t,0),⊙O半径为1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.在Rt△APK中,由∠PKA=90°,∠PAK=45°,PA=4,推出PK的值,在Rt△PEK中,根据勾股定理计算即可.
②分两种情形a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°;b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.分别列出方程求解即可.
试题解析:解:(1)∵y=﹣x+10的图象交x轴于点A,交y轴于点B,∴A(10,0),B(0,10),∴OA=OB=10.∵∠AOB=90°,∴∠OAB=∠OBA=45°.故答案分别为(10,0),(0,10),45°.
(2)由题意得:P(1+2t,0),⊙O半径为1+t.故答案为:(1+2t,0),1+t.
(3)①如图1中,作PK⊥AB于K,连接PE.
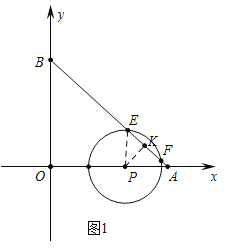
当t=![]() 时,P(6,0),半径为3.5,在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,∴PK=
时,P(6,0),半径为3.5,在Rt△APK中,∵∠PKA=90°,∠PAK=45°,PA=4,∴PK=![]() PA=
PA=![]() ,在Rt△PEK中,EK=
,在Rt△PEK中,EK=![]() =
=![]() ,∴EF=2EK=
,∴EF=2EK=![]() .
.
②存在.
a、如图2中,当点P在点A左侧时,点F与点A重合时,∠EPF=90°.
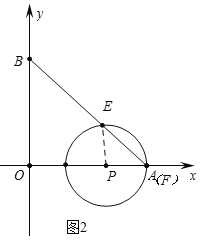
∵OP+PA=OA,∴1+2t+1+t=10,∴t=![]() .
.
b、如图3中,当点P在点A右侧时,点F与点A重合时,∠EPF=90°.
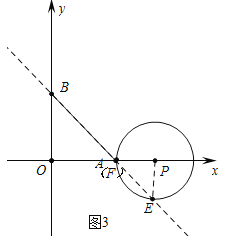
由OP﹣PF=OA,∴1+2t﹣(1+t)=10,∴t=10.
综上所述,t=![]() s或10s时,存在以点P为直角顶点的Rt△PEF.
s或10s时,存在以点P为直角顶点的Rt△PEF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是边AB上的动点,若在边AC,BC上分别有点E,F,使得
AE=AD,BF=BD.
(1)设∠C=α,求∠EDF(用含α的代数式表示);
(2)尺规作图:分别在边AB,AC上确定点P,Q(PQ不与DE平行或重合),使得
∠CPQ=∠EDF.(保留作图痕迹,不写作法)

-
科目: 来源: 题型:
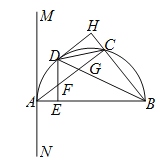
查看答案和解析>>【题目】如图,
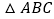 内接于半圆,
内接于半圆,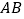 是直径,过
是直径,过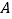 作直线
作直线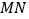 ,
,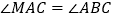 ,
,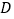 是弧
是弧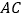 的中点,连接
的中点,连接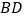 交
交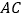 于
于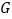 ,过
,过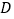 作
作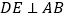 于
于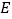 ,交
,交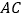 于
于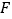 .
.
(
 )求证:
)求证: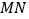 是半圆的切线.
是半圆的切线.(
 )作
)作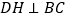 交
交 的延长线于点
的延长线于点 ,连接
,连接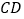 ,试判断线段
,试判断线段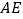 与线段
与线段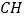 的数量关系,并说明理由.
的数量关系,并说明理由.(
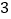 )若
)若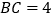 ,
,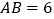 ,试求
,试求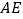 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E.则AD与BE平行吗?
完成下面的解答过程(填写理由或数学式).
解:∵∠1=∠2(已知),
∴ ∥ (内错角相等,两直线平行),
∴∠E=∠ (两直线平行,内错角相等),
又∵∠E=∠3(已知),
∴∠3=∠ (等量代换),
∴AD∥BE( ).

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图所示)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,根据图形可知他得出的这个推论指( )

A. S矩形ABMN=S矩形MNDCB. S矩形EBMF=S矩形AEFN
C. S矩形AEFN=S矩形MNDCD. S矩形EBMF=S矩形NFGD
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班从三名男生(含小强)和五名女生中选四名学生参加学校举行的“中华古诗文朗诵大赛”,规定女生选n名.
(1)当n为何值时,男生小强参加是确定事件?
(2)当n为何值时,男生小强参加是随机事件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱满金陵”慈善一日捐活动中,学校团总支为了了解本校写生的捐款情况,随机抽取了
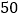 名学生的捐款数进行了统计,并绘制成统计图.
名学生的捐款数进行了统计,并绘制成统计图.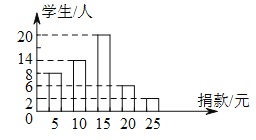
(
 )这
)这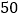 名同学捐款的众数为__________元,中位数为__________.
名同学捐款的众数为__________元,中位数为__________.(
 )求这
)求这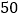 名同学捐款的平均数.
名同学捐款的平均数.(
 )该校共有
)该校共有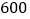 名学生参与捐款,请估计该校学生的捐款总数.
名学生参与捐款,请估计该校学生的捐款总数.
相关试题

