【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y= ![]() (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积为 ![]() .
.
参考答案:
【答案】
(1)
解:∵在矩形OABC中,OA=3,OC=2,
∴B(3,2),
∵F为AB的中点,
∴F(3,1),
∵点F在反比例函数y= ![]() (k>0)的图象上,
(k>0)的图象上,
∴k=3,
∴该函数的解析式为y= ![]() ;
;
(2)
解:由题意知E,F两点坐标分别为E( ![]() ,2),F(3,
,2),F(3, ![]() ),
),
∴S△EFA= ![]() AFBE=
AFBE= ![]() ×
× ![]() k(3﹣
k(3﹣ ![]() k),
k),
= ![]() k﹣
k﹣ ![]() k2
k2
∵△EFA的面积为 ![]() .
.
∴ ![]() k﹣
k﹣ ![]() k2=
k2= ![]() .
.
整理,得
k2﹣6k+8=0,
解得k1=2,k2=4,
∴当k的值为2或4时,△EFA的面积为 ![]() .
.
【解析】(1)当F为AB的中点时,点F的坐标为(3,1),由此代入求得函数解析式即可;(2)根据图中的点的坐标表示出三角形的面积,得到关于k的方程,通过解方程求得k的值即可.
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地开辟一块长方形的荒地用于新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 m2,那么:
(1)荒地的宽是多少?有1 000 m吗?(结果保留一位小数)
(2)如果要求结果保留整数,那么宽大约是多少?
(3)计划在该公园中心建一个圆形花圃,面积是800 m2,你能估计它的半径吗?(要求结果保留整数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列各组条件,不能判定△
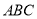 ≌△
≌△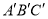 的一组是 ( )
的一组是 ( )A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.
(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;
(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
相关试题

