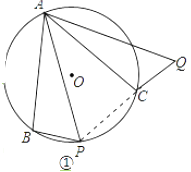
【题目】已知⊙O中,弦AB=AC,点P是∠BAC所对弧上一动点,连接PA,PB.
(1)如图①,把△ABP绕点A逆时针旋转到△ACQ,连接PC,求证:∠ACP+∠ACQ=180°;
(2)如图②,若∠BAC=60°,试探究PA、PB、PC之间的关系.
(3)若∠BAC=120°时,(2)中的结论是否成立?若是,请证明;若不是,请直接写出它们之间的数量关系,不需证明.
参考答案:
【答案】
(1)
证明:如图①,连接PC.
∵△ACQ是由△ABP绕点A逆时针旋转得到的,
∴∠ABP=∠ACQ.
由图①知,点A、B、P、C四点共圆,
∴∠ACP+∠ABP=180°(圆内接四边形的对角互补),
∴∠ACP+∠ACQ=180°(等量代换);
(2)
证明:解:PA=PB+PC.理由如下:
如图②,连接BC,延长BP至E,使PE=PC,连接CE.
∵弦AB=弦AC,∠BAC=60°,
∴△ABC是等边三角形(有一内角为60°的等腰三角形是等边三角形).
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°(圆内接四边形的对角互补),
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠ECP=∠EPC=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP(等量代换).
在△BEC和△APC中,  ,
,
∴△BEC≌△APC(SAS),
∴BE=PA,
∴PA=BE=PB+PC;

(3)
证明:若∠BAC=120°时,(2)中的结论不成立. ![]() PA=PB+PC.理由如下:
PA=PB+PC.理由如下:
如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.
∵∠BAC=120°,∠BAC+∠BPC=180°,
∴∠BPC=60°.
∵弦AB=弦AC,
∴∠APB=∠APQ=30°.
在△ABP和△AQP中,
∵  ,
,
∴△ABP≌△AQP(SAS),
∴AB=AQ,PB=PQ(全等三角形的对应边相等),
∴AQ=AC(等量代换).
在等腰△AQC中,QG=CG.
在Rt△APG中,∠APG=30°,则AP=2AG,PG= ![]() AG.
AG.
∴PB+PC=PG﹣QG+PG+CG=PG﹣QG+PG+QG=2PG=2 ![]() AG,
AG,
∴ ![]() PA=2
PA=2 ![]() AG,即
AG,即 ![]() PA=PB+PC.
PA=PB+PC.

【解析】(1)如图①,连接PC.根据“内接四边形的对角互补的性质”即可证得结论;(2)如图②,通过作辅助线BC、PE、CE(连接BC,延长BP至E,使PE=PC,连接CE)构建等边△PCE和全等三角形△BEC≌△APC;然后利用全等三角形的对应边相等和线段间的和差关系可以求得PA=PB+PC;(3)如图③,在线段PC上截取PQ,使PQ=PB,过点A作AG⊥PC于点G.利用全等三角形△ABP≌△AQP(SAS)的对应边相等推知AB=AQ,PB=PG,将PA、PB、PC的数量关系转化到△APC中来求即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)求一根A型跳绳和一根B型跳绳的售价各是多少元?
(2)学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于下列各组条件,不能判定△
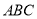 ≌△
≌△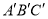 的一组是 ( )
的一组是 ( )A. ∠A=∠A′,∠B=∠B′,AB=A′B′
B. ∠A=∠A′,AB=A′B′,AC=A′C′
C. ∠A=∠A′,AB=A′B′,BC=B′C′
D. AB=A′B′,AC=A′C′,BC=B′C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
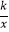 (k>0)的图象与BC边交于点E.
(k>0)的图象与BC边交于点E.
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积为 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标系xOy中,抛物线y=﹣x2+bx+c经过点A(﹣3,0)和B(1,0),与y轴交于点C,
(1)求抛物线的表达式;
(2)若点D为此抛物线上位于直线AC上方的一个动点,当△DAC的面积最大时,求点D的坐标;
(3)设抛物线顶点关于y轴的对称点为M,记抛物线在第二象限之间的部分为图象G.点N是抛物线对称轴上一动点,如果直线MN与图象G有公共点,请结合函数的图象,直接写出点N纵坐标t的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,y随x的增大而增大的是( )
A.y=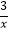
B.y=﹣x+5
C.y= x
x
D.y=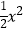 (x<0)
(x<0)
相关试题

