【题目】如图(1),Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D。AF平分∠CAB,交CD于点E,交CB于点F。

(1)求证:CE=CF。
(2)将图(1)中的△ADE沿AB向右平移到△A′D′E′的位置,使点E′落在BC边上,其它条件不变,如图(2)所示。试猜想:BE′与CF有怎样的数量关系?请证明你的结论。
参考答案:
【答案】(1)见解析证明;(2)![]() =CF.理由见解析证明.
=CF.理由见解析证明.
【解析】
试题分析:(1)根据角平分线的定义可得∠CAF=∠EAD,再根据等角的余角相等求出∠CFA=∠AED ,然后根据对顶角相等可得∠AED=∠CEF,从而得到∠CFA=∠AED,再根据等角对等边证明即可;(2)过点E作EG⊥AC于点G,根据角平分线的性质得到ED=EG,根据平移的性质可得![]() =DE,然后求出∠ACD=∠B,再利用“角角边”证明△CEG≌
=DE,然后求出∠ACD=∠B,再利用“角角边”证明△CEG≌![]() 全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
全等,根据全等三角形对应边相等可得BE′=CE,从而得到BE′=CF.
试题解析:(1)∵AF平分∠CAB,∴∠CAF=∠EAD,∵∠ACB=90°,∴∠CAF+∠CFA=90°,∵CD⊥AB,∴∠EAD+∠AED=90°, ∴∠CFA=∠AED ,又∵∠AED=∠CEF,∴∠CFA=∠AED,∴CE=CF;
(2)答:![]() =CF. 过点E作EG⊥AC于点G,
=CF. 过点E作EG⊥AC于点G,
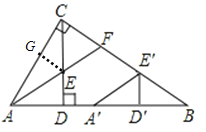
∵AF平分∠CAB,ED⊥AB,EG⊥AC,∴ED=EG,∵△ADE平移得到![]() ,∴
,∴![]() =DE,∴
=DE,∴![]() =GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和
=GE,∵∠ACB=90°,∴∠ACD+∠DCB=90°,∵CD⊥AB,∴∠B+∠DCB=90°,∴∠ACD=∠B,在△CEG和![]() 中,∵
中,∵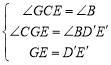 ,∴△CEG≌
,∴△CEG≌![]() (AAS),∴CE=
(AAS),∴CE=![]() ,又∵CE=CF,∴
,又∵CE=CF,∴![]() =CF.
=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】乐乐是一名健步运动的爱好者,她用手机软件记录了某个月(30天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
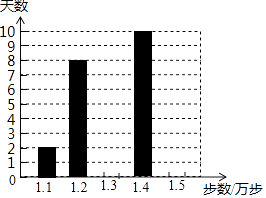
(1)若乐乐这个月平均每天健步走的步数为1.32万步,试求她走1.3万步和1.5万步的天数;
(2)求这组数据中的众数和中位数. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
3﹣
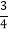 =3×
=3×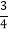 ;
;(﹣
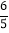 )﹣6=(﹣
)﹣6=(﹣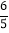 )×6;
)×6;(﹣0.5)﹣(﹣1)=(﹣0.5)×(﹣1)
根据上面这些等式反映的规律,解答下列问题:
(1)上面等式反映的规律用文字语言可以描述如下:存在两个有理数,使得这两个有理数的差等于
.
(2)若满足上述规律的两个有理数中有一个数是
 ,求另一个有理数;
,求另一个有理数;(3)若这两个有理数用字母a、b表示,则上面等式反映的规律用字母表示为 ;
(4)在(3)中的关系式中,字母a、b是否需要满足一定的条件?若需要,直接写出字母a、b应满足的条件;若不需要,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,M是等边△ABC边BC上的点,如图,连接AM,过点M作∠AMH=60°,MH与∠ACB的邻补角的平分线交于点H,过H作HD⊥BC于点D
(1)求证:MA=MH
(2)猜想写出CB、CM、CD之间的数量关系式,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
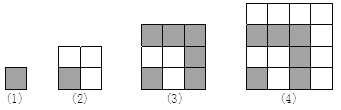 …
…第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形有1+3+5=9个小正方形;
第(4)个图形有25小正方形;
……
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n-1)的结果(用含n的代数式表示);
(2)请根据你的发现计算:① 1+3+5+7+…+99;
② 101+103+105+…+199.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市为鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费,月用水量不超过30立方米时,按2元/立方米计费;月用水量超过30立方米时,其中的30立方米仍按2元/立方米收费,超过部分按2.5元/立方米计费.设每户家庭月用水量为x立方米.
(1)当x不超过30时,应收多少水费(用x的代数式表示);当x超过30时,应收多少水费(用x的代数式表示);
(2)小明家四月份用水20立方米,五月份用水36立方米,请帮小明计算一下他家这两个月一共应交多少元水费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:如图(1),在数轴上A示的数为a,B点表示的数为b,则点A到点B的距离记为AB.线段AB的长可以用右边的数减去左边的数表示,即AB=b-a.
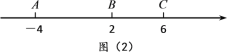
解决问题:如图(2),数轴上点A表示的数是-4,点B表示的数是2,点C表示的数是6.
(1)若数轴上有一点D,且AD=3,求点D表示的数;
(2)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.求点A表示的数(用含t的代数式表示),BC等于多少(用含t的代数式表示).
(3)请问:3BC-AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
相关试题

