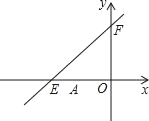
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() .点
.点![]() 的坐标为(
的坐标为(![]() ,0),点
,0),点![]() 的坐标为(
的坐标为(![]() ,0).
,0).
(1)求![]() 的值;
的值;
(2)若点![]() (
(![]() ,
,![]() )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.

参考答案:
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
试题(1)将点E坐标(-8,0)代入直线y=kx+6就可以求出k值,从而求出直线的解析式;
(2)由点A的坐标为(-6,0)可以求出OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式就可以表示出△OPA.从而求出其关系式;根据P点的移动范围就可以求出x的取值范围.
(3)根据△OPA的面积为![]() 代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
代入(2)的解析式求出x的值,再求出y的值就可以求出P点的位置.
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,
∴k=![]() ;
;
(2)∵k=![]() ,
,
∴直线的解析式为:y=![]() x+6,
x+6,
∵P点在y=![]() x+6上,设P(x,
x+6上,设P(x,![]() x+6),
x+6),
∴△OPA以OA为底的边上的高是|![]() x+6|,
x+6|,
当点P在第二象限时,|![]() x+6|=
x+6|=![]() x+6,
x+6,
∵点A的坐标为(﹣6,0),
∴OA=6.
∴S=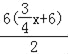 =
=![]() x+18.
x+18.
∵P点在第二象限,
∴﹣8<x<0;
(3)设点P(m,n)时,其面积S=![]() ,
,
则![]() ,
,
解得|n|=![]() ,
,
则n1=![]() 或者n2=﹣
或者n2=﹣![]() (舍去),
(舍去),
当n=![]() 时,
时,![]() =
=![]() m+6,
m+6,
则m=﹣![]() ,
,
故P(﹣![]() ,
,![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线
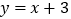 的图象与x轴、y轴交于A,B两点,直线
的图象与x轴、y轴交于A,B两点,直线 经过原点,与线段AB交于点C,把
经过原点,与线段AB交于点C,把 的面积分为2:1的两部分,求直线
的面积分为2:1的两部分,求直线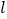 的解析式.
的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c,OA=OC,下列关系中正确的是( )

A.ac+1=b
B.ab+1=c
C.bc+1=a
D.
+1=c -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: ①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2 .
其中一定正确的是( )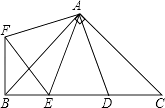
A.②④
B.①③
C.①④
D.②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售
 ,
, 两种型号的新能源汽车。上周售出1辆
两种型号的新能源汽车。上周售出1辆 型车和3辆
型车和3辆 型车,销售额为96万元,本周已售出2辆
型车,销售额为96万元,本周已售出2辆 型车和1辆
型车和1辆 型车,销售额为62万元。
型车,销售额为62万元。(1)求每辆
 型车和
型车和 型车的售价各为多少?
型车的售价各为多少?(2)随着汽车限购政策的推行,预计下周起
 ,
, 两种型号的汽车价格在原有的基础均有上涨,若
两种型号的汽车价格在原有的基础均有上涨,若 型汽车价格上涨m%,
型汽车价格上涨m%, 型汽车价格上涨3m%,则同时购买一台
型汽车价格上涨3m%,则同时购买一台 型车和一台
型车和一台 型车的费用比涨价前多12%,求
型车的费用比涨价前多12%,求 的值.
的值. -
科目: 来源: 题型:
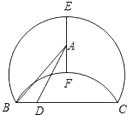
查看答案和解析>>【题目】如图,点E,F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A,D分别为线段EF,BC上的动点.连接AB,AD,设BD=x,AB2﹣AD2=y,下列图像中,能表示y与x的函数关系的图像是( )
A.
B.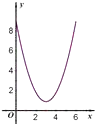
C.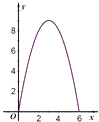
D.
-
科目: 来源: 题型:
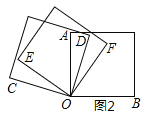
查看答案和解析>>【题目】(1)如图1,将两个正方形(每个角都是
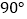 )的一个顶点重合放置,若
)的一个顶点重合放置,若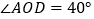 ,求
,求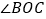 的度数;
的度数;(2)如图2,将三个正方形的一个顶点重合放置,若
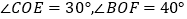 ,求
,求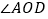 的度数;
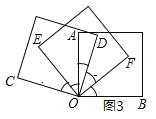
的度数;(3)如图3,将三个正方形的一个顶点重合放置,若
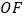 平分
平分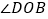 ,那么
,那么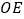 平分
平分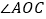 吗?为什么?
吗?为什么?
相关试题

