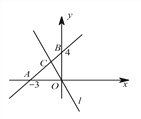
【题目】如图所示,已知直线![]() 的图象与x轴、y轴交于A,B两点,直线
的图象与x轴、y轴交于A,B两点,直线![]() 经过原点,与线段AB交于点C,把
经过原点,与线段AB交于点C,把![]() 的面积分为2:1的两部分,求直线
的面积分为2:1的两部分,求直线![]() 的解析式.
的解析式.
参考答案:
【答案】![]() 或
或![]() .
.
【解析】分析:根据直线y=x+4的解析式可求出A、B两点的坐标,如图:
(1)当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;
(2)当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,同(1).
详解:由直线y=x+3的解析式可求得A(-3,0)、B(0,3),
如图(1),当直线l把△AOB的面积分为S△AOC:S△BOC=2:1时,

作CF⊥OA于F,CE⊥OB于E,则S△AOB=![]() ,则S△AOC=3,
,则S△AOC=3,
∴![]() AOCF=3,即
AOCF=3,即![]() ×3×CF=3,
×3×CF=3,
∴CF=2.
同理,解得CE=1.
∴C(-1,2),
∴直线l的解析式为y=-2x;
如图(2),当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,

同理求得C(-2,1),
∴直线l的解析式为y=-![]() x.
x.
故答案为y=-2x或y=-![]() x.
x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C.
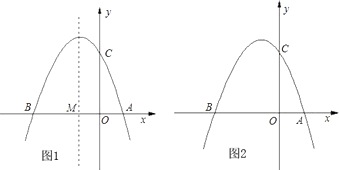
(1)求抛物线的解析式;
(2)设抛物线的对称轴与x轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由;
(3)如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(3)班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
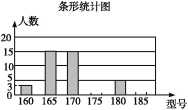
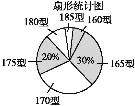
根据以上信息,解答下列问题:
(1)该班共有多少名学生?其中穿175型校服的学生有多少人?
(2)在条形统计图中,请把空缺的部分补充完整;
(3)在扇形统计图中,请计算185型校服所对应扇形圆心角的大小;
(4)求该班学生所穿校服型号的众数和中位数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:
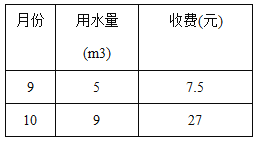
设某户每月用水量x(立方米),应交水费y(元)
(1)a= ,c=
(2)当x≤6,x≥6时,分别求出y于x的函数关系式
(3)若该户11月份用水量为8立方米,求该户11 月份水费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c,OA=OC,下列关系中正确的是( )

A.ac+1=b
B.ab+1=c
C.bc+1=a
D.
+1=c -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论: ①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2 .
其中一定正确的是( )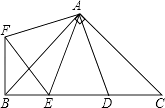
A.②④
B.①③
C.①④
D.②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
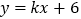 与
与 轴、
轴、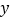 轴分别交于点
轴分别交于点 ,
, .点
.点 的坐标为(
的坐标为(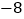 ,0),点
,0),点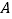 的坐标为(
的坐标为(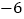 ,0).
,0).(1)求
 的值;
的值;(2)若点
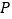 (
( ,
,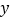 )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点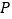 运动过程中,试写出
运动过程中,试写出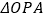 的面积
的面积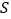 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)探究:当
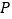 运动到什么位置时,
运动到什么位置时,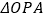 的面积为
的面积为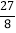 ,并说明理由.
,并说明理由.
相关试题

