【题目】(1)如图1,将两个正方形(每个角都是![]() )的一个顶点重合放置,若
)的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
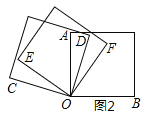
(2)如图2,将三个正方形的一个顶点重合放置,若![]() ,求
,求![]() 的度数;
的度数;
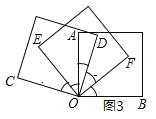
(3)如图3,将三个正方形的一个顶点重合放置,若![]() 平分
平分![]() ,那么
,那么![]() 平分
平分![]() 吗?为什么?
吗?为什么?

参考答案:
【答案】(1)140°(2)20°(3)OE平分![]()
【解析】
(1)根据正方形各角等于90°,得出∠COD+∠AOB=180°,再根据∠AOD=40°,∠COB=∠COD+∠AOB-∠AOD,即可得出答案;
(2)根据已知得出∠1+∠2,∠1+∠3的度数,再根据∠1+∠2+∠3=90°,最后用∠1+∠2+∠1+∠3-(∠1+∠2+∠3),即可求出∠1的度数;
(3)根据∠COD=∠AOB和等角的余角相等得出∠COA=∠DOB,∠EOA=∠FOB,再根据角平分线的性质得出∠DOF=∠FOB=![]() ∠DOB和∠EOA=
∠DOB和∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,从而得出答案.
∠COA,从而得出答案.
(1)∵两个图形是正方形,
∴∠COD=90°,∠AOB=90°,
∴∠COD+∠AOB=180°,
∵∠AOD=40°,
∴∠COB=∠COD+∠AOB-∠AOD=140°
故答案为:140;
(2)如图,由题意知,∠1+∠2=50°①,
∠1+∠3=60°②,
又∠1+∠2+∠3=90°③,
①+②-③得∠1=20°;
(3)OE平分∠AOC,理由如下:
∵∠COD=∠AOB,
∴∠COA=∠DOB(等角的余角相等),
同理:∠EOA=∠FOB,
∵OF平分∠DOB,
∴∠DOF=∠FOB=![]() ∠DOB,
∠DOB,
∴∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,
∠COA,
∴OE平分∠AOC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
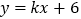 与
与 轴、
轴、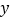 轴分别交于点
轴分别交于点 ,
, .点
.点 的坐标为(
的坐标为(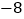 ,0),点
,0),点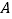 的坐标为(
的坐标为(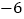 ,0).
,0).(1)求
 的值;
的值;(2)若点
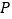 (
( ,
,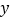 )是第二象限内的直线上的一个动点.当点
)是第二象限内的直线上的一个动点.当点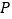 运动过程中,试写出
运动过程中,试写出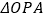 的面积
的面积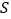 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)探究:当
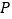 运动到什么位置时,
运动到什么位置时,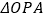 的面积为
的面积为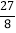 ,并说明理由.
,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售
 ,
, 两种型号的新能源汽车。上周售出1辆
两种型号的新能源汽车。上周售出1辆 型车和3辆
型车和3辆 型车,销售额为96万元,本周已售出2辆
型车,销售额为96万元,本周已售出2辆 型车和1辆
型车和1辆 型车,销售额为62万元。
型车,销售额为62万元。(1)求每辆
 型车和
型车和 型车的售价各为多少?
型车的售价各为多少?(2)随着汽车限购政策的推行,预计下周起
 ,
, 两种型号的汽车价格在原有的基础均有上涨,若
两种型号的汽车价格在原有的基础均有上涨,若 型汽车价格上涨m%,
型汽车价格上涨m%, 型汽车价格上涨3m%,则同时购买一台
型汽车价格上涨3m%,则同时购买一台 型车和一台
型车和一台 型车的费用比涨价前多12%,求
型车的费用比涨价前多12%,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E,F是以线段BC为公共弦的两条圆弧的中点,BC=6.点A,D分别为线段EF,BC上的动点.连接AB,AD,设BD=x,AB2﹣AD2=y,下列图像中,能表示y与x的函数关系的图像是( )
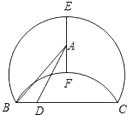
A.
B.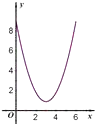
C.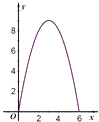
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
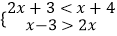 ,并在数轴上表示解集.
,并在数轴上表示解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·西宁)(本小题满分7分)给出三个整式a2,b2和2ab.
(1)当a=3,b=4时,求a2+b2+2ab的值;
(2)在上面的三个整式中任意选择两个整式进行加法或减法运算,使所得的多项式能够因式分解.请写也你所选的式子及因式分解的过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
相关试题

