【题目】已知函数f(x)= ![]() ,若关于x的不等式f2(x)+af(x)>0恰有两个整数解,则实数a的取值范围是( )
,若关于x的不等式f2(x)+af(x)>0恰有两个整数解,则实数a的取值范围是( )
A.(﹣ ![]() ,﹣
,﹣ ![]() )
)
B.[ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,﹣
,﹣ ![]() ]
]
D.(﹣1,﹣ ![]() ]
]
参考答案:
【答案】C
【解析】解:∵f′(x)= ![]() , ∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
, ∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
当a>0时,f2(x)+af(x)>0f(x)<﹣a或f(x)>0,此时不等式f2(x)+af(x)>0有无数个整数解,不符合题意;
当a=0时,f2(x)+af(x)>0f(x)≠0,此时不等式f2(x)+af(x)>0有无数个整数解,不符合题意;
当a<0时,f2(x)+af(x)>0f(x)<0或f(x)>﹣a,要使不等式f2(x)+af(x)>0恰有两个整数解,必须满足
f(3)≤﹣a<f(2),得 ![]() <a≤
<a≤ ![]() ,
,
故选:C.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆ρ=4cosθ与圆ρ=2sinθ交于O,A两点. (Ⅰ)求直线OA的斜率;
(Ⅱ)过O点作OA的垂线分别交两圆于点B,C,求|BC|. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|. (Ⅰ)解不等式:f(x)+f(x﹣1)≤2,;
(Ⅱ)若a>0,求证:f(ax)﹣af(x)≤f(a). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
 ,则
,则 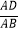 =( )
=( )
A.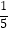
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数列{an}中,a2n=a2n﹣1+(﹣1)n , a2n+1=a2n+n,a1=1则a100= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的内角A、B、C的对边分别为a、b、c,且3bcos A=ccos A+acosC.
(1)求tanA的值;
(2)若a=4 ,求△ABC的面积的最大值.
,求△ABC的面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某同学在研究性学习中,收集到某制药厂今年前5个月甲胶囊生产产量(单位:万盒)的数据如下表所示:
月份x
1
2
3
4
5
y(万盒)
4
4
5
6
6
(1)该同学为了求出y关于x的线性回归方程 =
=  +
+  ,根据表中数据已经正确计算出
,根据表中数据已经正确计算出  =0.6,试求出
=0.6,试求出  的值,并估计该厂6月份生产的甲胶囊产量数;
的值,并估计该厂6月份生产的甲胶囊产量数;
(2)若某药店现有该制药厂今年二月份生产的甲胶囊4盒和三月份生产的甲胶囊5盒,小红同学从中随机购买了3盒甲胶囊,后经了解发现该制药厂今年二月份生产的所有甲胶囊均存在质量问题.记小红同学所购买的3盒甲胶囊中存在质量问题的盒数为ξ,求ξ的分布列和数学期望.
相关试题

