【题目】在平面直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,圆ρ=4cosθ与圆ρ=2sinθ交于O,A两点. (Ⅰ)求直线OA的斜率;
(Ⅱ)过O点作OA的垂线分别交两圆于点B,C,求|BC|.
参考答案:
【答案】解:(Ⅰ)由 ![]() ,得2cosθ=sinθ,tanθ=2, ∴kOA=2.
,得2cosθ=sinθ,tanθ=2, ∴kOA=2.
(Ⅱ)设A的极角为θ,tanθ=2,则sinθ= ![]() ,cosθ=
,cosθ= ![]() ,则B(ρ1 , θ﹣
,则B(ρ1 , θ﹣ ![]() ),代入ρ=2cosθ得ρ1=2cos(θ﹣
),代入ρ=2cosθ得ρ1=2cos(θ﹣ ![]() )=2sinθ=
)=2sinθ= ![]() ,
,
C(ρ2 , θ+ ![]() ),代代入ρ=sinθ得ρ2=sin(θ+
),代代入ρ=sinθ得ρ2=sin(θ+ ![]() )=cosθ=
)=cosθ= ![]() ,
,
∴|BC|=ρ1+ρ2= ![]()
【解析】(Ⅰ)由由 ![]() ,得2cosθ=sinθ,化简即可得出kOA . (Ⅱ)设A的极角为θ,tanθ=2,则sinθ=
,得2cosθ=sinθ,化简即可得出kOA . (Ⅱ)设A的极角为θ,tanθ=2,则sinθ= ![]() ,cosθ=
,cosθ= ![]() ,把B(ρ1 , θ﹣
,把B(ρ1 , θ﹣ ![]() )代入ρ=2cosθ得ρ1 . 把C(ρ2 , θ+
)代入ρ=2cosθ得ρ1 . 把C(ρ2 , θ+ ![]() )代入ρ=sinθ得ρ2 , 利用|BC|=ρ1+ρ2 , 即可得出.
)代入ρ=sinθ得ρ2 , 利用|BC|=ρ1+ρ2 , 即可得出.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,
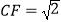 .
. 
(1)求证:BC⊥平面ACFE;
(2)点M在线段EF上运动,设平面MAB与平面FCB二面角的平面角为θ(θ≤90°),试求cosθ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】己知抛物线C1:x2=2py(p>0)与圆C2:x2+y2=5的两个交点之间的距离为4. (Ⅰ)求p的值;
(Ⅱ)设过抛物线C1的焦点F且斜率为k的直线与抛物线交于A,B两点,与圆C2交于C,D两点,当k∈[0,1]时,求|AB||CD|的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
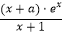 (e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(e为自然对数的底数),曲线y=f(x)在(1,f(1))处的切线与直线4x+3ey+1=0互相垂直. (Ⅰ)求实数a的值;
(Ⅱ)若对任意x∈( ,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
,+∞),(x+1)f(x)≥m(2x﹣1)恒成立,求实数m的取值范围;
(Ⅲ)设g(x)=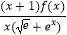 ,Tn=1+2[g(
,Tn=1+2[g( 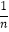 )+g(
)+g( 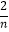 )+g(
)+g( 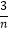 )+…+g(
)+…+g( 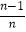 )](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有
)](n=2,3…).问:是否存在正常数M,对任意给定的正整数n(n≥2),都有 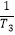 +
+ 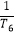 +
+ 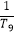 +…+
+…+ 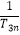 <M成立?若存在,求M的最小值;若不存在,请说明理由.
<M成立?若存在,求M的最小值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=|x﹣1|. (Ⅰ)解不等式:f(x)+f(x﹣1)≤2,;
(Ⅱ)若a>0,求证:f(ax)﹣af(x)≤f(a). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
 ,则
,则 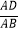 =( )
=( )
A.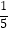
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,若关于x的不等式f2(x)+af(x)>0恰有两个整数解,则实数a的取值范围是( )
,若关于x的不等式f2(x)+af(x)>0恰有两个整数解,则实数a的取值范围是( )
A.(﹣ ,﹣
,﹣  )
)
B.[ ,
,  )
)
C.(﹣ ,﹣
,﹣  ]
]
D.(﹣1,﹣ ]
]
相关试题

