【题目】某中学计划购买A型和B型课桌凳共200套. 经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,且购买4套A型和5套B型课桌凳共需1820元.(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)、学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
参考答案:
【答案】(1)、A型180元,B型220元;(2)、3种方案;费用最低方案:A型80套,B型120套.
【解析】
试题分析:(1)、首先设A型每套x元,则B型每套(x+40)元,总费用1820元列出方程求出x的值,从而得出答案;(2)、首先设购买A型课桌凳a套,则购买B型课桌凳(200-a)套,根据购买的数量和总价列出不等式组,从而得出a的取值范围,得出购买的方案.设总费用为y,然后得出y与a的函数关系式,根据一次函数的增减性得出y取最小值时a的值.
试题解析:(1)、设A型每套x元,则B型每套(x+40)元. ∴4x+5(x+40)=1820. ∴x=180,x+40=220.
即购买一套A型课桌凳和一套B型课桌凳各需180元、220元.
(2)、设购买A型课桌凳a套,则购买B型课桌凳(200-a)套.
∴ 解得78≤a≤80. ∵a为整数,∴a = 78,79,80
解得78≤a≤80. ∵a为整数,∴a = 78,79,80
∴共有3种方案.
设购买课桌凳总费用为y元,则y=180a+220(200-a)=-40a+44000
∵-40<0,y随a的增大而减小,∴当a=80时,总费用最低,此时200-a=120.
即总费用最低的方案是:购买A型80套,购买B型120套.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列逆命题是真命题的是( )
A.如果x=y,那么x2=y2
B.相等的角是内错角
C.有三个角是60°的三角形是等边三角形
D.全等三角形的对应角相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(1)﹣3m+2m﹣5m;(2)(2a2﹣1+2a)﹣(a﹣1+a2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提倡“绿色”出行,顺义区启动了公租自行车项目,为了解我区居民公租自行车的使用情况,某校的社团把使用情况分为A(经常租用)、B(偶尔租用)、C(不使用)三种情况.先后在2015年1月底和3月底做了两次调查,并根据调查结果绘制成了如下两幅不完整的统计图:

根据以上信息解答下列问题:
(1)在扇形统计图中,A(经常租用)所占的百分比是 ;
(2)求两次共抽样调查了多少人;并补全折线统计图;
(3)根据调查的结果,请你谈谈从2015年1月底到2015年3月底,我区居民使用公租自行车的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”
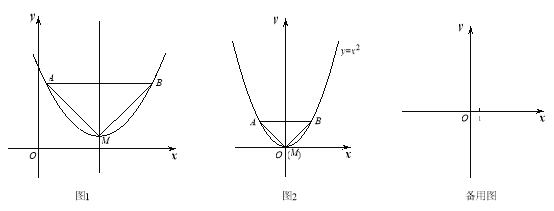
(1)①如图2,求出抛物线
 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;②抛物线
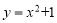 与
与 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;(2)若抛物线
 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;(3)若抛物线
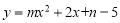 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且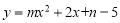 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.

(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
相关试题

